辽宁省营口市2019届中考适应性考试数学试卷

试卷更新日期：2019-12-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 有理数﹣ $\frac{1}{2}$ 的倒数是（）

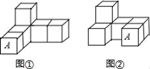
A、 $\frac{1}{2}$ B、﹣2 C、2 D、1

查看试题解析
2. 如图，是由6个棱长为1个单位的正方体摆放而成的，将正方体A向右平移2个单位，向后平移1个单位后，所得几何体的视图（）

A、主视图改变，俯视图改变 B、主视图不变，俯视图改变 C、主视图不变，俯视图不变 D、主视图改变，俯视图不变

查看试题解析
3. 下列计算正确的是

A、a²·a²＝2a⁴ B、(－a²)³＝－a⁶ C、3a²－6a²＝3a² D、(a－2)²＝a²－4

查看试题解析
4. 在一次体操比赛中，六位评委对某位选手的打分（单位：分）如下：9.2，9.4，9.1，9.3，9.2，9.6，这组数据的平均数和众数分别为（）

A、9.3 9.2 B、9.2 9.2 C、9.2 9.3 D、9.3 9.6

查看试题解析
5. 关于x的一元二次方程x²+x+1＝0的根的情况是（）

A、两个不等的实数根 B、两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
6. 如图，在△ABC中，AB＝AC，∠BAC＝45°，将△ABC绕点A逆时针方向旋转得△AEF，其中，E，F是点B，C旋转后的对应点，BE，CF相交于点D.若四边形ABDF为菱形，则∠CAE的大小是（）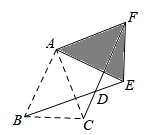

A、45° B、60° C、75° D、90°

查看试题解析
7. 如图，△ABC中AB两个顶点在x轴的上方，点C的坐标是（﹣1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C′，且△A′B′C′与△ABC的位似比为2：1.设点B的对应点B′的横坐标是a，则点B的横坐标是（）

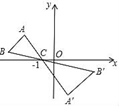A、 $- \frac{1}{2} a$ B、 $- \frac{1}{2} (a + 1)$ C、 $- \frac{1}{2} (a - 1)$ D、 $- \frac{1}{2} (a + 3)$

查看试题解析
8. 对于一次函数y＝（k﹣3）x+2，y随x的增大而增大，k的取值范围是（）

A、k＜0 B、k＞0 C、k＜3 D、k＞3

查看试题解析
9. 如图，在△ABC中，BA=BC，BP，CQ是△ABC的两条中线，M是BP上的一个动点，则下列线段的长等于AM+QM最小值的是（）

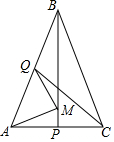A、AC B、CQ C、BP D、BC

查看试题解析
10. 如图1.已知正△ABC中，E，F，G分别是AB，BC，CA上的点，且AE＝BF＝CG，设△EFG的面积为y，AE的长为x，y关于x的函数图象如图2，则△EFG的最小面积为（）

A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{\sqrt{3}}{2}$ C、2 D、 $\sqrt{3}$

查看试题解析

二、填空题

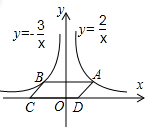
11. 将数12000000科学记数法表示为．

查看试题解析
12. 函数y＝ $\sqrt{3 - x}$ 的自变量x的取值范围是．

查看试题解析
13. 在一次摸球实验中，摸球箱内放有白色、黄色乒乓球共50个，这两种乒乓球的大小、材质都相同.小明发现，摸到白色乒乓球的频率稳定在60%左右，则箱内黄色乒乓球的个数很可能是.

查看试题解析
14. 如图，点A是反比例函数的图象上任意一点，轴交反比例函数的图象于点B，以AB为边作平行四边形ABCD，其中C、D在x轴上，则四边形ABCD的面积为.

查看试题解析
15. 如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为2和1，若用阴影部分围成一个圆锥，则该圆锥的底面半径为.

查看试题解析
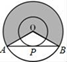16. 某工程队依据城市规划轨道交通计划，为地铁二号线修建一条长4800米的隧道.在打通1200米隧道后，为了尽快减少施工对城市交通造成的影响，该工程队增加了人力，故现在每天打通隧道的长度是原来的1.2倍，最终40天完成任务.若设该工程队原来每天打通隧道x米，则列出的方程为：.

查看试题解析
17. 如图，在矩形ABCD中，AB＝8，AD＝4，点E、F分别在线段AD、AB上，将△AEF沿EF翻折，使得点A落在矩形ABCD内部的P点，连接PD，当△PDE是等边三角形时，BF的长为.

查看试题解析
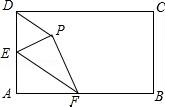18. 如图，点O（0，0），A（0，1）是正方形OAA₁B的两个顶点，以OA₁对角线为边作正方形OA₁A₂B₁ ，再以正方形的对角线OA₂作正方形OA₁A₂B₁ ， …，依次规律，则点A₈的坐标是.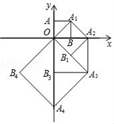

查看试题解析

三、解答题

19. 计算

(1)、（﹣1）²⁰¹⁷﹣（ $\frac{1}{3}$ ）^﹣¹+ $\sqrt[3]{8}$

(2)、（1+ $\frac{1}{x - 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，其中x＝﹣5.

查看试题解析
20. 小明家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，按下任意一个开关均可打开对应的一盏电灯，因刚搬进新房不久，不熟悉情况.

(1)、若小明任意按下一个开关，则下列说法正确的是 .

A、小明打开的一定是楼梯灯 B、小明打开的可能是卧室灯 C、小明打开的不可能是客厅灯 D、小明打开走廊灯的概率是 $\frac{1}{3}$

(2)、若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明.

查看试题解析
21. 某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动，将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.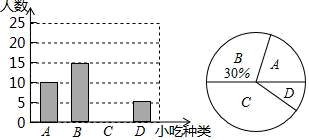

调查问卷：在下面四种泰兴美食中，你最喜爱的是（）(单选)

A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝

请根据所给信息解答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、补全条形统计图，并计算扇形统计图中“A”部分所对应的圆心角的度数为；

(3)、若全校有1200名学生，请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人？

查看试题解析
22. 在一次数学综合实践活动中，小明计划测量城门大楼的高度，在点B处测得楼顶A的仰角为22°，他正对着城楼前进21米到达C处，再登上3米高的楼台D处，并测得此时楼顶A的仰角为45°.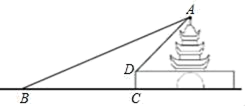

(1)、求城门大楼的高度；

(2)、每逢重大节日，城门大楼管理处都要在A，B之间拉上绳子，并在绳子上挂一些彩旗，请你求出A，B之间所挂彩旗的长度（结果保留整数）.（参考数据：sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$ ）

查看试题解析
23. 如图，以AB为直径的⊙O外接于△ABC，点D在BC的延长线上，∠ABC的角平分线与AD交于E点，与AC交于F点，且AE＝AF.

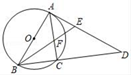(1)、证明直线AD是⊙O的切线；

(2)、若AD＝16，sinD＝ $\frac{4}{5}$ ，求BC的长.

查看试题解析
24. 某市实施产业精准扶贫，帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克，到了收获季节投入市场销售时，调查市场行情后，发现该蜜柚不会亏本，且每天的销售量y（千克）与销售单价x（元）之间的函数关系如图所示.

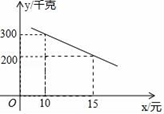(1)、求y与x的函数关系式，并写出x的取值范围；

(2)、当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

(3)、某村农户今年共采摘蜜柚12000千克，若该品种蜜柚的保质期为50天，按照（2）的销售方式，能否在保质期内全部销售完这批蜜柚？若能，请说明理由；若不能，应定销售价为多少元时，既能销售完又能获得最大利润？

查看试题解析
25. 已知如图 1，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， $B C = A C$ ，点 $D$ 在 $A B$ 上， $D E ⊥ A B$ 交 $B C$ 于 $E$ ，点 $F$ 是 $A E$ 的中点.

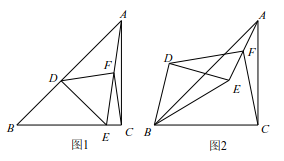(1)、写出线段 $F D$ 与线段 $F C$ 的关系并证明；

(2)、如图，将 $Δ B D E$ 绕点 $B$ 逆时针旋转 $α (0 ° < α < 90 °)$ ，其它条件不变，线段 $F D$ 与线段 $F C$ 的关系是否变化，写出你的结论并证明；

(3)、将 $Δ B D E$ 绕点 $B$ 逆时针旋转一周，如果 $B C = 4 ， B E = 2 \sqrt{2}$ ，直接写出线段 $B F$ 的范围.

查看试题解析
26. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{1}{2}$ x+2分别交x轴、y轴于点A、B.点C的坐标是（﹣1，0），抛物线y＝ax²+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点，过点P作x轴的垂线交直线AB于点M，交抛物线于点Q，连结DQ，设点P的横坐标为m（m≠0）.

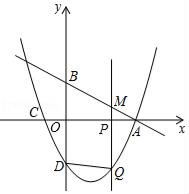(1)、求点A的坐标.

(2)、求抛物线的表达式.

(3)、当以B、D、Q，M为顶点的四边形是平行四边形时，求m的值.

查看试题解析