辽宁省朝阳市2019届九年级中考适应性考试数学试卷（一）

试卷更新日期：2019-12-30 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2019}$ 的倒数是（）

A、﹣2019 B、 $- \frac{1}{2019}$ C、 $\frac{1}{2019}$ D、2019

查看试题解析
2. 如图所示是机器零件的立体图，从上面看到的平面图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，计算正确的是（）

A、（a²b）³=a⁵b³ B、（3a²）³=27a⁶ C、x⁶÷x²=x³ D、（a+b）²=a²+b²

查看试题解析
4. 下列事件中，属于必然事件的是（　　）

A、“世界杯新秀”姆巴佩发点球 100%进球 B、任意购买一张车票，座位刚好挨着窗口 C、三角形内角和为 180° D、叙利亚不会发生战争

查看试题解析
5. 如图，在△ABC中，D，E分别在边AC与AB上，DE∥BC，BD、CE相交于点O， $\frac{E O}{O C} = \frac{1}{3}$ ，AE＝1，则EB的长为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 体育课上，20人一组进行足球比赛，每人射点球5次，已知某一组的进球总数为49个，进球情况记录如下表，其中进2个球的有x人，进3个球的有y人，由题意列出关于x与y的方程组为（　　）

进球数

0

1

2

3

4

5

人数

1

5

x

y

3

2

A、 ${\begin{matrix} x + y = 9 \\ 2 x + 3 y = 22 \end{matrix}$ B、 ${\begin{matrix} x + y = 20 \\ 3 x + 2 y = 49 \end{matrix}$ C、 ${\begin{matrix} y - x = 1 \\ x + y = 29 \end{matrix}$ D、 ${\begin{matrix} x + y = 22 \\ 2 x + 3 y = 9 \end{matrix}$

查看试题解析
7. 某车间20名工人每天加工零件数如表所示：

每天加工零件数

4

5

6

7

8

人数

3

6

5

4

2

这些工人每天加工零件数的众数、中位数分别是（）

A、5，5 B、5，6 C、6，6 D、6，5

查看试题解析
8. 如图，在矩形ABCD中，AB＝2，BC＝4，把矩形折叠，使点D与点B重合，点C落在点E处，则折痕FG的长为（　　）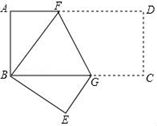

A、2.5 B、3 C、 $\sqrt{5}$ D、2 $\sqrt{5}$

查看试题解析
9. 下列关于二次函数 $y = 2 x^{2}$ 的说法正确的是（）

A、它的图象经过点 $(- 1, - 2)$ B、它的图象的对称轴是直线 $x = 2$ C、当 $x < 0$ 时， $y$ 随 $x$ 的增大而减小 D、当 $x = 0$ 时， $y$ 有最大值为0

查看试题解析
10. 如图，点E、F分别为正方形ABCD的边BC、CD上一点，AC、BD交于点O，且∠EAF＝45°，AE，AF分别交对角线BD于点M，N，则有以下结论：①△AOM∽△ADF；②EF＝BE+DF；③∠AEB＝∠AEF＝∠ANM；④S_△_AEF＝2S_△_AMN ，以上结论中，正确的个数有（　）个.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 将数12000000科学记数法表示为．

查看试题解析
12. 如图，已知AB是⊙O的弦，C是 $\overset{⌢}{A B}$ 的中点，联结OA，AC，如果∠OAB＝20°，那么∠CAB的度数是.

查看试题解析
13. 如图，△ABC中，D、E、F分别是各边的中点，随机地向△ABC中内掷一粒米，则米粒落到阴影区域内的概率是.

查看试题解析
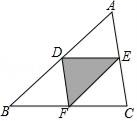14. 任意写出一个3的倍数 $($ 例如： $111)$ ，首先把这个数各数位上的数字都立方，再相加，得到一个新数，然后把这个新数重复上述运算，运算结果最终会得到一个固定不变的数M，它会掉入一个数字“黑洞” $.$ 那么最终掉入“黑洞”的那个数M是.

查看试题解析
15. 如图，已知正比例函数y＝kx（k≠0）和反比例函数y＝ $\frac{m}{x}$ （m≠0）的图象相交于点A（﹣2，1）和点B，则不等式kx＜ $\frac{m}{x}$ 的解集是.

查看试题解析
16. 已知某果农贩卖的西红柿，其质量与价钱成一次函数关系，今小华向果农买一竹篮的西红柿，含竹篮称得总质量为15公斤，付西红柿的钱25元.若他再加买0.5公斤的西红柿，需多付1元，则空竹篮的质量为公斤.

查看试题解析

三、解答题

17. 计算： $4 \sin 60^{°} - | - 1 | + {(\sqrt{3} - 1)}^{0} + \sqrt{48}$

查看试题解析
18. 先化简： $\frac{a^{2} - 1}{a^{2} - 2 a + 1} \div \frac{a + 1}{a - 1} - \frac{a}{a - 1}$ ;再在不等式组 ${\begin{matrix} 3 - (a + 1) > 0 \\ 2 a + 2 \geq 0 \end{matrix}$ 的整数解中选取一个合适的解作为a的取值，代入求值.

查看试题解析
19. 《如果想毁掉一个孩子，就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上，法国教育部宣布从2018年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人.

请你根据以上信息解答下列问题：

(1)、在扇形统计图中，“玩游戏”对应的百分比为，圆心角度数是度；

(2)、补全条形统计图；

(3)、该校共有学生2100人，估计每周使用手机时间在2小时以上（不含2小时）的人数.

查看试题解析
20. 如图所示，一艘轮船在近海处由西向东航行，点C处有一灯塔，灯塔附近30海里的圆形区域内有暗礁，轮船在A处测得灯塔在北偏东60°方向上，轮船又由A向东航行40海里到B处，测得灯塔在北偏东30°方向上.

(1)、求轮船在B处时到灯塔C处的距离是多少？

(2)、若轮船继续向东航行，有无触礁危险？

查看试题解析
21. 在三个完全相同的小球上分别写上-2，-1，2三个数字，然后装入一个不透明的布袋内搅匀，从布袋中取出一个球，记下小球上的数字为 $m$ ，放回袋中再搅匀，然后再从袋中取出一个小球，记下小球上的数字为 $n$ ，组成一对数 $(m ， n)$ .

(1)、请用列表或画树状图的方法，表示出数对 $(m ， n)$ 的所有可能的结果；

(2)、求直线 $y = m x + n$ 不经过第一象限的概率.

查看试题解析
22. 如图，AB为⊙O直径，C、D为⊙O上的点，∠ACD＝2∠A，CE⊥DB交DB的延长线于点E.

(1)、求证：直线CE与⊙O相切；

(2)、若AC＝8，AB＝10，求CE的长.

查看试题解析
23. 在矩形ABCD中，AB＝6，AD＝8，点E是边AD上一点，EM⊥EC交AB于点M，点N在射线MB上，且AE是AM和AN的比例中项.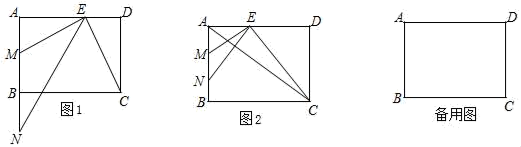

(1)、如图1，求证：∠ANE＝∠DCE；

(2)、如图2，当点N在线段MB之间，联结AC，且AC与NE互相垂直，求MN的长；

(3)、连接AC，如果△AEC与以点E、M、N为顶点所组成的三角形相似，求DE的长.

查看试题解析
24. 如图1，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax²+bx+5与x轴交于A，点B，与y轴交于点C，过点C作CD⊥y轴交抛物线于点D，过点B作BE⊥x轴，交DC延长线于点E，连接BD，交y轴于点F，直线BD的解析式为y＝﹣x+2.

(1)、写出点E的坐标；抛物线的解析式.

(2)、如图2，点P在线段EB上从点E向点B以1个单位长度/秒的速度运动，同时，点Q在线段BD上从点B向点D以 $\sqrt{2}$ 个单位长度/秒的速度运动，当一个点到达终点时，另一个点随之停止运动，当t为何值时，△PQB为直角三角形？

(3)、如图3，过点B的直线BG交抛物线于点G，且tan∠ABG＝ $\frac{1}{2}$ ，点M为直线BG上方抛物线上一点，过点M作MH⊥BG，垂足为H，若HF＝MF，请直接写出满足条件的点M的坐标.

查看试题解析

进球数	0	1	2	3	4	5
人数	1	5	x	y	3	2

每天加工零件数	4	5	6	7	8
人数	3	6	5	4	2