广东省阳江市阳东区2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 观察如图图形，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线y=3（x﹣2）²+5的顶点坐标是（）

A、（﹣2，5） B、（﹣2，﹣5） C、（2，5） D、（2，﹣5）

查看试题解析
3. 若点A（﹣1，6）在反比例函数y＝ $\frac{k}{x}$ 的图象上，则k的值是（）

A、﹣6 B、﹣2 C、2 D、6

查看试题解析
4. 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD ，垂足为点E ，连接CO ， AD ，则下列说法中不一定成立的是（）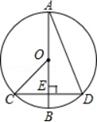

A、CE＝DE B、∠BOC＝2∠BAD C、弧AC=弧AD D、AD＝2CE

查看试题解析
5. 对于反比例函数 $y = - \frac{2}{x}$ ，下列说法错误的是 $($ $)$

A、图象分布在第二、四象限 B、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 C、图象经过点（1，-2） D、若点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 都在图象上，且 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$

查看试题解析
6. 下列说法中正确的是（）

A、“任意画出一个平行四边形，它是中心对称图形”是必然事件 B、“任意画出一个等边三角形，它是轴对称图形”是随机事件 C、“概率为0.0001的事件”是不可能事件 D、任意掷一枚质地均匀的硬币10次，正面向上的一定是5次

查看试题解析
7. 如图，正方形ABCD的边长为1，弧CE，弧EF 的圆心分别为D、A两点，则CF的长为（）

A、1 B、 $\sqrt{3}$ C、3 D、 $\sqrt{10}$

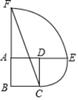查看试题解析
8. 如图，在▱APBC中，∠C＝40°，若⊙O与PA、PB相切于点A、B ，则∠CAB＝（）

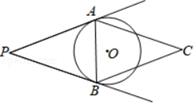A、40° B、50° C、60° D、70°

查看试题解析
9. 二次函数y＝ax²+bx+c（a ， b ， c为常数，且a≠0）中的x与y的部分对应值如表：

x

﹣1

0

1

3

y

﹣1

3

5

3

有下列结论：

①ac＜0；②当x＞1时，y的值随x值的增大而减小；③x＝3是方程ax²+（b﹣1）x+c＝0的一个根；④当﹣1＜x＜3时，ax²+（b﹣1）x+c＞0．小明从中任意选取一个结论，则选中符合题意结论的概率为（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

10. 在平面直角坐标系中，点P（2，﹣3）关于原点对称点P′的坐标是．

查看试题解析
11. 已知关于x方程x²﹣3x+a=0有一个根为1，则方程的另一个根为．

查看试题解析
12. 如图，在平行四边形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为.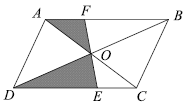

查看试题解析
13. 如图，将△ABC绕点A逆时针旋转90°得到△ADE ，点C和点E是对应点，若AB＝1，则BD＝．

查看试题解析
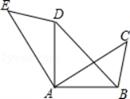14. 已知A（﹣4，y₁），B（﹣1，y₂）是反比例函数y=﹣ $\frac{4}{x}$ 图象上的两个点，则y₁与y₂的大小关系为．

查看试题解析
15. 如图，在扇形AOB中，∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为4时，阴影部分的面积为．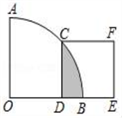

查看试题解析

三、解答题

16. 解方程：3x（x﹣1）＝x﹣1．

查看试题解析
17. 如图，△ABC与△ADE都是等腰直角三角形，连接CD、BE ， CD、BE相交于点O ， △BAE可看作是由△CAD顺时针旋转所得．

(1)、旋转中心是，旋转角度是；

(2)、判断CD与BE的位置关系，并说明理由．

查看试题解析
18. 如图，已知抛物线y＝﹣x²+bx+c的部分图象，A（1，0），B（0，3）．

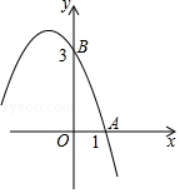(1)、求抛物线的解析式；

(2)、若抛物线与x轴的另一个交点是C点，求△ABC的面积．

查看试题解析
19. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E ，连接AD ， BC ， CO

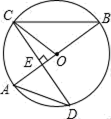(1)、当∠BCO＝25°时，求∠A的度数；

(2)、若CD＝4 $\sqrt{2}$ ，BE＝4，求⊙O的半径．

查看试题解析
20. 已知关于x的方程x²+mx+m-2=0.

(1)、若此方程的一个根为1,求m的值；

(2)、求证：不论m取何实数,此方程都有两个不相等的实数根.

查看试题解析
21. 小方与小辉在玩军棋游戏，他们定义了一种新的规则，用军棋中的“工兵”、“连长”、“地雷”比较大小，共有6个棋子，分别为1个“工兵”，2个“连长”，3个“地雷”游戏规则如下：①游戏时，将棋反面朝上，两人随机各摸一个棋子进行比赛，先摸者摸出的棋不放回；②“工兵”胜“地雷”，“地雷”胜“连长”，“连长”胜“工兵”；③相同棋子不分胜负.

(1)、若小方先摸，则小方摸到“排长”的事件是；若小方先摸到了“连长”，小辉在剩余的5个棋子中随机摸一个，则这一轮中小方胜小辉的概率为.

(2)、如果先拿走一个“连长”，在剩余的5个棋子中小方先摸一个棋子，然后小辉在剩余的4个棋子中随机摸一个，求这一轮中小方获胜的概率.

查看试题解析
22. 如图，一次函数 $y = m x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A (3 ， 1)$ ， $B (- \frac{1}{2}$ ， $n)$ 两点．

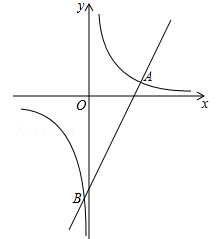(1)、求该反比例函数的解析式；

(2)、求 $n$ 的值及该一次函数的解析式．

查看试题解析
23. 在Rt△ABC中，∠ACB＝90°，BE平分∠ABC ， D是边AB上一点，以BD为直径的⊙O经过点E ，且交BC于点F ．

(1)、求证：AC是⊙O的切线；

(2)、若BF＝6，⊙O的半径为5，求CE的长．

查看试题解析
24. 某厂家生产一种新型电子产品，制造时每件的成本为40元，通过试销发现，销售量 $y ($ 万件 $)$ 与销售单价 $x ($ 元 $)$ 之间符合一次函数关系，其图象如图所示.

(1)、求y与x的函数关系式；

(2)、物价部门规定：这种电子产品销售单价不得超过每件80元，那么，当销售单价x定为每件多少元时，厂家每月获得的利润 $(w)$ 最大？最大利润是多少？

查看试题解析

x	﹣1	0	1	3
y	﹣1	3	5	3