湖北省襄阳市襄州区2019届中考适应性考试数学试卷（二）

试卷更新日期：2019-12-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 比﹣1大1的数是（）

A、﹣2 B、0 C、2 D、3

查看试题解析
2. 计算(x²)²的结果是（）

A、x² B、x⁴ C、x⁶ D、x⁸

查看试题解析
3. 习近平主席在2018年新年贺词中指出，“安得广厦千万间，大庇天下寒士俱欢颜！”2017年，340万贫困人口实现易地扶贫搬迁，有了温暖的新家，各类棚户区改造开工提前完成600万套目标任务.将340万用科学记数法表示为（）

A、 $0.34 \times 10^{7}$ B、 $34 \times 10^{5}$ C、 $3.4 \times 10^{5}$ D、 $3.4 \times 10^{6}$

查看试题解析
4. 已知a为整数，且 $\sqrt{3} < a < \sqrt{5}$ ，则a等于（）

A、1 B、2 C、3 D、4

查看试题解析
5. 在平面直角坐标系中，点A的坐标是(1，3)，将点A绕原点O顺时针旋转90°得到点A′，则点A′的坐标是（）

A、(﹣3，1) B、(3，﹣1) C、(﹣1，3) D、(1，﹣3)

查看试题解析
6. 如图，矩形ABCD的边AB＝1，BC＝2，以点B为圆心，BC为半径画弧，交AD于点E，则图中阴影部分的面积是（）

A、 $\frac{4 - \sqrt{3}}{2}$ $- \frac{π}{3}$ B、2 $- \sqrt{3} - \frac{π}{3}$ C、 $\frac{4 - \sqrt{3}}{2}$ $- \frac{π}{6}$ D、2﹣ $\sqrt{3} - \frac{π}{6}$

查看试题解析

二、填空题

7. 一个正数a的平方根分别是2m﹣1和﹣3m+ $\frac{5}{2}$ ，则这个正数a为．

查看试题解析
8. 若x，y为实数，y= $\frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}} + 1}{x - 2}$ ，则4y﹣3x的平方根是．

查看试题解析
9. 如果 ${(2 + \sqrt{2})}^{2} = a + b \sqrt{2}$ (a，b为有理数)，则a＝， b＝．

查看试题解析
10. 把多项式ax²﹣2ax+a分解因式的结果是．

查看试题解析
11. 某组数据按从小到大的顺序如下：2、4、8、x、10、14，已知这组数据的中位数是9，则这组数据的众数是.

查看试题解析
12. 已知关于x的方程5x²+kx﹣6＝0的一个根2，则k＝，另一个根为．

查看试题解析
13. 已知直线 y=ax（a≠0）与反比例函数 y= $\frac{k}{x}$ （k≠0）的图象一个交点坐标为（2，4），则它们另一个交点的坐标是．

查看试题解析
14. 如图，在△ABC中，AC＝BC，把△ABC沿AC翻折，点B落在点D处，连接BD，若∠CBD＝16°，则∠BAC＝°．

查看试题解析
15. 如图，在⊙O的内接五边形ABCDE中，∠B+∠E＝210°，则∠CAD＝°．

查看试题解析
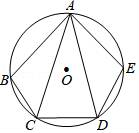16. 如图，在四边形ABCD中，AD∥BC (BC＞AD)，∠D＝90°，∠ABE＝45°，BC＝CD，
若AE＝5，CE=2，则BC的长度为．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} x - 1 \geq 2 x \\ \frac{x - 1}{2} \leq \frac{x}{3} \end{array}$

查看试题解析
18. 先化简，再求值：（ $\frac{x^{2} - 2 x + 1}{x^{2} - x}$ + $\frac{x^{2} - 4}{x^{2} + 2 x}$ ）÷ $\frac{1}{x}$ ，且x为满足﹣3＜x＜2的整数．

查看试题解析
19. 某中学组织学生去离学校15km的农场，先遣队与大队同时出发，先遣队的速度是大队的速度的1.2倍，结果先遣队比大队早到0.5h，先遣队和大队的速度各是多少？

查看试题解析

20. 某校为了了解全校400名学生参加课外锻炼的情况，随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查，结果如下：（单位：分）

40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45

(1)、补全频率分布表和频率分布直方图．

分组	频数	频率
4.5﹣22.5	2	0.050
22.5﹣30.5	3
30.5﹣38.5	10	0.250
38.5﹣46.5	19
46.5﹣54.5	5	0.125
54.5﹣62.5	1	0.025
合计	40	1.000

(2)、填空：在这个问题中，总体是，样本是．由统计结果分析的，这组数据的平均数是38.35（分），众数是，中位数是．

(3)、如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况，你认为用平均数、众数、中位数中的哪一个量比较合适？

(4)、估计这所学校有多少名学生，平均每天参加课外锻炼的时间多于30分？

查看试题解析

21. 有两把不同的锁和三把不同的钥匙，其中两把钥匙分别能打开这两把锁，第三把钥匙不能打开这两把锁，随机取出一把钥匙开任意一把锁，一次打开锁的概率是多少？

查看试题解析
22. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．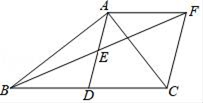

(1)、求证：△AEF≌△DEB；

(2)、若∠BAC＝90°，求证：四边形ADCF是菱形．

查看试题解析
23. 如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°．且D离地面的高度DE＝5m．坡底EA＝30m，然后在A处测得建筑物顶端B的仰角是60°，点E，A，C在同一水平线上，求建筑物BC的高．(结果用含有根号的式子表示)

查看试题解析
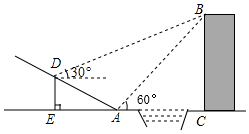24. 有一个二次函数满足以下条件：①函数图象与x轴的交点坐标分别为A(1，0)，B(x₂ ， y₂)(点B在点A的右侧)；②对称轴是x＝3；③该函数有最小值是﹣2．

(1)、请根据以上信息求出二次函数表达式；

(2)、将该函数图象x＞x₂的部分图象向下翻折与原图象未翻折的部分组成图象“G”，平行于x轴的直线与图象“G”相交于点C(x₃ ， y₃)、D(x₄ ， y₄)、E(x₅ ， y₅)(x₃＜x₄＜x₅)，结合画出的函数图象求x₃+x₄+x₅的取值范围．

查看试题解析
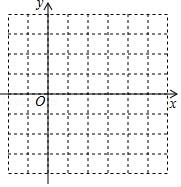25. 已知：如图，在Rt△ABC中，∠C＝90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交于点D，E，且∠CBD＝∠A．

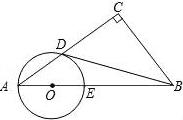(1)、判断直线BD与⊙O的位置关系，并证明你的结论；

(2)、若AD：AO＝8：5，BC＝2，求BD的长．

查看试题解析
26. 某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．设甲、乙两车间各自加工大米数量y（吨）与甲车间加工时间s（天）之间的关系如图（1）所示；未加工大米w（吨）与甲加工时间x（天）之间的关系如图（2）所示，请结合图象回答下列问题：

(1)、甲车间每天加工大米吨，a= ．

(2)、求乙车间维修设备后，乙车间加工大米数量y（吨）与x（天）之间函数关系式．

(3)、若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？

查看试题解析
27. 如图，矩形ABCD中，AB＝4，BC＝m(m＞1)，点E是AD边上一定点，且AE＝1．

(1)、当m＝3时，AB上存在点F，使△AEF与△BCF相似，求AF的长度．

(2)、如图②，当m＝3.5时．用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F．(不写作法，保留作图痕迹)

(3)、对于每一个确定的m的值，AB上存在几个点F，使得△AEF与△BCF相似？

查看试题解析