湖北省武汉市黄陂区2019届数学中考模拟试卷(4月)
试卷更新日期:2019-12-30 类型:中考模拟
一、单选题
-
1. 在数轴上点M表示的数为 ,与点M距离等于3个单位长度的点表示的数为A、1 B、 C、 或1 D、 或52. 若分式 有意义,则x的取值范围是( )A、x≠﹣3 B、x≥﹣3 C、x≠﹣3且 x≠2 D、x≠23. 如图,两个面积分别为35,23的图形叠放在一起,两个阴影部分的面积分别为a,b(a>b),则a-b的值为( )
 A、6 B、8 C、9 D、124. 据统计,我市今年十一月份日平均气温的分布情况如下表:
A、6 B、8 C、9 D、124. 据统计,我市今年十一月份日平均气温的分布情况如下表:平均气温(℃)
13
14
15
16
17
天数
3
7
3
9
8
其中频数最高的气温(℃)是( )
A、17 B、16 C、15 D、145. 下列计算正确的是( )A、b4•b4=2b4 B、(x3)3=x6 C、70×8﹣2= D、(﹣bc)4÷(﹣bc)2=﹣b2c26.如图,边长均为1个单位的正方形组成的方格纸内有一张笑脸图案,已知左眼的坐标是(﹣1,0),那么右眼关于鼻子所在的水平线对称的点的坐标是( )
 A、(1,﹣2) B、(1,﹣1) C、(﹣1,0) D、(﹣1,﹣2)7. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
A、(1,﹣2) B、(1,﹣1) C、(﹣1,0) D、(﹣1,﹣2)7. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )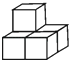 A、
A、 B、
B、 C、
C、 D、
D、 8. 某市6月份日平均气温统计如图所示,那么在日平均气温这组数据中,中位数是( )
8. 某市6月份日平均气温统计如图所示,那么在日平均气温这组数据中,中位数是( ) A、8 B、10 C、21 D、229. 如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A、8 B、10 C、21 D、229. 如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )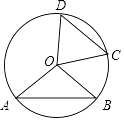 A、6 B、8 C、5 D、5
A、6 B、8 C、5 D、5二、填空题
-
10. 计算:11. 如果 ,那么代数式 的值是.12. 某航班每次飞行约有100名乘客,若飞机失事的概率为p=0.000 05,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿40万元人民币. 平均来说,保险公司应向每位乘客至少收取元保险费才能保证不亏本.13. 如图,直角梯形ABCD中,AD∥BC,∠ADC=∠BAC=90°,AB=2,CD= ,则AD的长为.
 14. 在平面直角坐标系xOy中,已知点P(﹣2,1)关于y轴的对称点P′,点T(t,0)是x轴上的一个动点,当△P′TO是等腰三角形时,t的值是.15. 已知二次函数y=x2﹣2x+m的图象与x轴交于A,B两点,若点A坐标为(﹣1,0),则点B的坐标为.
14. 在平面直角坐标系xOy中,已知点P(﹣2,1)关于y轴的对称点P′,点T(t,0)是x轴上的一个动点,当△P′TO是等腰三角形时,t的值是.15. 已知二次函数y=x2﹣2x+m的图象与x轴交于A,B两点,若点A坐标为(﹣1,0),则点B的坐标为.三、解答题
-
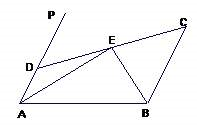
16. 解方程组: .17. 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
 18. 朗读者 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级 、 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩 满分为100分 如图所示.
18. 朗读者 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级 、 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩 满分为100分 如图所示.平均数
中位数
众数
九 班
85
85
九 班
80
 (1)、根据图示填写表格;(2)、结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)、如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.19. 每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买了3台甲型设备比购买2台乙型设备多花了16万元,购买2台甲型设备比购买3台乙型设备少花6万元.(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.20. 已知, 内接于 ,点 是弧 的中点,连接 、 ;
(1)、根据图示填写表格;(2)、结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)、如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.19. 每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买了3台甲型设备比购买2台乙型设备多花了16万元,购买2台甲型设备比购买3台乙型设备少花6万元.(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.20. 已知, 内接于 ,点 是弧 的中点,连接 、 ; (1)、如图1,若 ,求证: ;(2)、如图2,若 平分 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.21. 如图,在平面直角坐标系中,反比例函数 (x>0,k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)、如图1,若 ,求证: ;(2)、如图2,若 平分 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.21. 如图,在平面直角坐标系中,反比例函数 (x>0,k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C. (1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求直线AB的函数解析式.22. 如图,点O为矩形ABCD的对称中心,AB=5cm,BC=6cm,点E.F.G分别从A.B.C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E.F.G运动的时间为t(单位:s).
(1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求直线AB的函数解析式.22. 如图,点O为矩形ABCD的对称中心,AB=5cm,BC=6cm,点E.F.G分别从A.B.C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E.F.G运动的时间为t(单位:s). (1)、当t等于多少s时,四边形EBFB′为正方形;(2)、若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)、是否存在实数t,使得点B’与点O重合?若存在,求出t的值;若不存在,请说明理由.23. 如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线 ( )过E,A′两点.
(1)、当t等于多少s时,四边形EBFB′为正方形;(2)、若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)、是否存在实数t,使得点B’与点O重合?若存在,求出t的值;若不存在,请说明理由.23. 如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线 ( )过E,A′两点. (1)、填空:∠AOB=°,用m表示点A′的坐标:A′( , );(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P,且 时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
(1)、填空:∠AOB=°,用m表示点A′的坐标:A′( , );(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P,且 时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.