广东省深圳市宝安区2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的几何体中，俯视图为三角形的是（）

A、 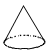B、 C、 D、

查看试题解析
2. 一元二次方程 ${(x - 2)}^{2} = 0$ 的根是 $($ $)$

A、 $x = 2$ B、 $x_{1} = x_{2} = 2$ C、 $x_{1} = - 2$ ， $x_{2} = 2$ D、 $x_{1} = 0$ ， $x_{2} = 2$

查看试题解析
3. 如图，在矩形ABCD中，对角线AC，BD交于点O，若∠COD＝50°，那么∠CAD的度数是（）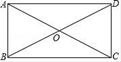

A、20° B、25° C、30° D、40°

查看试题解析
4. 已知 $- 1$ 是一元二次方程 ${ax}^{2} + bx + 1 = 0$ 的一个根，则 $a - b$ 的值是 $($ $)$

A、 $- 1$ B、0 C、1 D、无法确定

查看试题解析
5. 已知菱形的面积为10，对角线的长分别为x和y，则y关于x的函数图象是 $($ $)$

A、 B、 C、 D、

查看试题解析
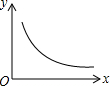6. 在不透明的袋子里装有16个红球和若干个白球，这些球除颜色不同外无其它差别 $.$ 每次从袋子里摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到白球的频率稳定在 $0.6$ ，则袋中白球有 $($ $)$

A、12个 B、20个 C、24个 D、40个

查看试题解析
7. 如图，这是某市政道路的交通指示牌．BD的距离为3m ，从D点测得指示牌顶端A点和底端C点的仰角分别是60°和45°，则指示牌的高度，即AC的长度是（）

A、3 $\sqrt{3}$ B、3 $\sqrt{2}$ C、3 $\sqrt{3}$ ﹣3 $\sqrt{2}$ D、3 $\sqrt{3}$ ﹣3

查看试题解析
8. 下列说法正确的是 $($ $)$

A、两条对角线互相垂直且相等的四边形是正方形 B、任意两个等腰三角形相似 C、一元二次方程 $x^{2} - ax - 2 = 0$ ，无论a取何值，一定有两个不相等的实数根 D、关于反比例函数 $y = \frac{4}{x}$ ，y的值随x值的增大而减小

查看试题解析
9. 如图，已知△ABO与△DCO位似，且△ABO与△DCO的面积之比为1：4，点B的坐标为(﹣3，2)，则点C的坐标为（）

A、(3，﹣2) B、(6，﹣4) C、(4，﹣6) D、(6，4)

查看试题解析
10. 如图，在菱形ABCD中，∠A＝60°，AB＝2，点M为边AD的中点，连接BD交CM于点N ，则BN的长是（）

A、1 B、 $\frac{4}{3}$ C、 $\sqrt{3}$ D、 $\frac{2}{3} \sqrt{3}$

查看试题解析
11. 二次函数 $y = {ax}^{2} + bx + c$ 的图象如图所示，以下结论中正确的是 $($ $)$

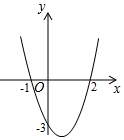A、 $abc < 0$ B、 $4 ac - b^{2} > 0$ C、当 $x < 1$ 时，y随x的增大而减小 D、 $4 a - 2 b + c > 0$

查看试题解析
12. 如图，矩形ABCD， $AB = 8$ ， $AD = 14$ ，点M，N分别为边AD和边BC上的两点，且 $MN / / AB$ ，点E是点A关于MN所在的直线的对称点，取CD的中点F，连接EF，NF，分别将 $△ EDF$ 沿着EF所在的直线折叠，将 $△ CNF$ 沿着NF所在的直线折叠，点D和点C恰好重合于EN上的点 $G .$ 以下结论中：
$① EF ⊥ NF$ ； $② ∠ MNE = ∠ CNE$ ； $③ △ MNE$ ∽ $△ DEF$ ； $④$ 四边形MNCD是正方形； $⑤ AM = 5.$ 其中正确的结论是 $($ $)$

A、 $① ②$ B、 $① ④$ C、 $① ③ ⑤$ D、 $① ④ ⑤$

查看试题解析

二、填空题

13. 已知 $\frac{x}{2} = \frac{y}{5}$ ，则 $\frac{2 x - y}{x} =$ ．

查看试题解析
14. 抛物线y＝x²﹣6x+5向上平移3个单位长度，再向左平移2个单位长度后，得到的抛物线解析式是．

查看试题解析
15. 如图，在A时测得一棵大树的影长为4米，B时又测得该树的影长为6米，若两次日照的光线互相垂直，则树的高度是．

查看试题解析
16. 如图，在平面直角坐标系中，直线y＝ $\frac{1}{3}$ x与双曲线y＝ $\frac{k}{x}$ （k≠0）交于点A，过点C（0，2）作AO的平行线交双曲线于点B，连接AB并延长与y轴交于点D（0，4），则k的值为.

查看试题解析

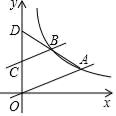
三、解答题

17. 天猫商城某网店销售某款蓝牙耳机，进价为100元 $.$ 在元旦即将来临之际，开展了市场调查，当蓝牙耳机销售单价是180元时，平均每月的销售量是200件，若销售单价每降低2元，平均每月就可以多售出10件．

(1)、设每件商品降价x元，该网店平均每月获得的利润为y元，请写出y与x元之间的函数关系；

(2)、该网店应该如何定价才能使得平均每月获得的利润最大，最大利润是多少元？

查看试题解析
18. 计算： $- 12 + {(\sqrt{7})}^{2} + cos 45^{\circ} + | 1 - \sqrt{2} |$

查看试题解析
19. 有3张正面分别写有数字 $- 2$ ，0，1的卡片，它们的背面完全相同，现将这3张卡片背面朝上洗匀，小明先从中任意抽出一张卡片记下数字为x；小亮再从剩下的卡片中任意取出一张记下数字为y，记作 $P (x, y)$ ．

(1)、用列表或画树状图的方法列出所有可能的点P的坐标；

(2)、若规定：点 $P (x, y)$ 在第二象限小明获胜；点 $P (x, y)$ 在第四象限小亮获胜，游戏规则公平吗？

查看试题解析
20. 如图，一次函数 $y_{1} = - x + 2$ 的图象与反比例函数 $y_{2} = \frac{k}{x} (k \neq 0)$ 的图象分别交于第二、四象限的A，B两点，点A的横坐标为 $- 1$ ．

(1)、求反比例函数的表达式；

(2)、根据图象回答：当x取何值时， $y_{1} < y_{2} .$ 请直接写出答案：．

查看试题解析
21. 如图，在平行四边形ABCD中， $AC ⊥ AD$ ，延长DA于点E，使得 $DA = AE$ ，连接BE．

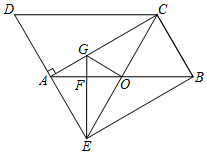(1)、求证：四边形AEBC是矩形；

(2)、过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若 $AB = 6$ ， $∠ CAB = 30^{\circ}$ ，求 $△ OGC$ 的面积．

查看试题解析
22. 如图，在矩形ABCD中， $AB = 4$ ， $BC = 2$ ，点E是边BC的中点 $.$ 动点P从点A出发，沿着AB运动到点B停止，速度为每秒钟1个单位长度，连接PE，过点E作PE的垂线交射线AD与点Q，连接PQ，设点P的运动时间为t秒．

(1)、当 $t = 1$ 时， $sin ∠ PEB =$ ；

(2)、是否存在这样的t值，使 $△ APQ$ 为等腰直角三角形？若存在，求出相应的t值，若不存在，请说明理由；

(3)、当t为何值时， $△ PEQ$ 的面积等于10？

查看试题解析
23. 如图，抛物线 $y = x^{2} + bx + c$ 与x轴相交于A，B两点，与y轴相交于点C，已知抛物线的对称轴所在的直线是 $x = \frac{9}{4}$ ，点B的坐标为 $(4 ， 0)$

(1)、抛物线的解析式是；

(2)、若点P是直线BC下方抛物线上一动点，当 $∠ ABP = 2 ∠ ABC$ 时，求出点P的坐标；

(3)、若M为x轴上一动点，在抛物线上是否存在点N，使得点B，C，M，N构成的四边形是菱形？若存在，求出N点的坐标；若不存在，请说明理由．

查看试题解析