广东省茂名市高州市2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 下列各式中是一元二次方程的是( )A、x2+1= B、x(x+1)=x2﹣3 C、2x2+3x﹣1 D、﹣x2+3x﹣1=02. 下列四条线段中,不能成比例的是( )A、a=4,b=8,c=5,d=10 B、a=2,b=2 ,c= ,d=5 C、a=1,b=2,c=3,d=4 D、a=1,b=2,c=2,d=43. 某校幵展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )A、 B、 C、 D、4. 如图所示的某零件左视图是( )
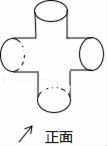 A、
A、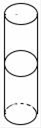 B、
B、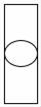 C、
C、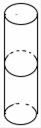 D、
D、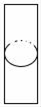 5. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,BD=8,则OE长为( )
5. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,BD=8,则OE长为( )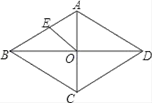 A、3 B、5 C、2.5 D、46. 已知点M(﹣3,4)在双曲线y= 上,则下列各点在该双曲线上的是( )A、(3,4) B、(﹣4,﹣3 ) C、(4,3 ) D、(3,﹣4)7. 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC , 若AD:DB=3:2,则AE:AC等于( )
A、3 B、5 C、2.5 D、46. 已知点M(﹣3,4)在双曲线y= 上,则下列各点在该双曲线上的是( )A、(3,4) B、(﹣4,﹣3 ) C、(4,3 ) D、(3,﹣4)7. 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC , 若AD:DB=3:2,则AE:AC等于( ) A、3:2 B、3:1 C、2:3 D、3:58. 如图,反比例函数y1= 和正比例函数y2═k2x的图象交于A(﹣2,﹣3),B(2,3)两点.若 >k2x,则x的取值范围是( )
A、3:2 B、3:1 C、2:3 D、3:58. 如图,反比例函数y1= 和正比例函数y2═k2x的图象交于A(﹣2,﹣3),B(2,3)两点.若 >k2x,则x的取值范围是( ) A、﹣2<x<0 B、﹣2<x<2 C、x<﹣2或0<x<2 D、﹣2<x<0 或x>29. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣2,1)或(2,﹣1) D、(﹣8,4)或(8,﹣4)10. 已知关于x的方程(k﹣2)2x2+(2k+1)x+1=0有实数解,且反比例函数y= 的图象经过第二、四象限,若k是常数,则k的值为( )A、4 B、3 C、2 D、1
A、﹣2<x<0 B、﹣2<x<2 C、x<﹣2或0<x<2 D、﹣2<x<0 或x>29. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣2,1)或(2,﹣1) D、(﹣8,4)或(8,﹣4)10. 已知关于x的方程(k﹣2)2x2+(2k+1)x+1=0有实数解,且反比例函数y= 的图象经过第二、四象限,若k是常数,则k的值为( )A、4 B、3 C、2 D、1二、填空题
-
11. 若|a+2|+b2﹣2b+1=0,则a2b+ab2= .12. 甲、乙、丙3人站成一排合影留念,甲站在中间的概率为 .13. 已知方程3x2﹣4x﹣2=0的两个根是x1、x2 , 则 = .14. 若线段a,b,c满足关系 , ,则a:b:c= .15. 如图,菱形ABCD中,∠B=60°,AB=3,四边形ACEF是正方形,则EF的长为 .
 16. 如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF= .
16. 如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF= .
三、解答题
-
17. 用适当的方法解下列方程:3x2+2x=2.18. 如图是一个正三棱柱的俯视图:
 (1)、你请作出它的主、左视图;(2)、若AC=2,AA'=3,求左视图的面积.19. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、你请作出它的主、左视图;(2)、若AC=2,AA'=3,求左视图的面积.19. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: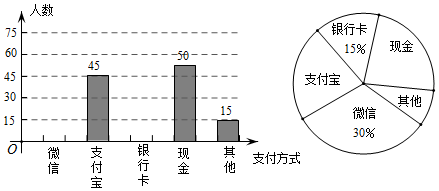 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.20. 已知关于x的一元二次方程kx2﹣6x+1=0有两个不相等的实数根.(1)、求实数k的取值范围;(2)、写出满足条件的k的最大整数值,并求此时方程的根.21. 如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BD)为2.7米,则他测得的树高应为多少米?
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.20. 已知关于x的一元二次方程kx2﹣6x+1=0有两个不相等的实数根.(1)、求实数k的取值范围;(2)、写出满足条件的k的最大整数值,并求此时方程的根.21. 如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BD)为2.7米,则他测得的树高应为多少米? 22. 已知:如图,平行四边形 的对角线相交于点 ,点 在边 的延长线上,且 ,联结 .
22. 已知:如图,平行四边形 的对角线相交于点 ,点 在边 的延长线上,且 ,联结 . (1)、求证: ;(2)、如果 ,求证: .23. 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.(1)、如果多种5棵橙子树,计算每棵橙子树的产量;(2)、如果果园橙子的总产量要达到60375个,考虑到既要成本低,又要保证树与树间的距离不能过密,那么应该多种多少棵橙子树;(3)、增种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?24. 如图,已知双曲线 ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)、求证: ;(2)、如果 ,求证: .23. 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.(1)、如果多种5棵橙子树,计算每棵橙子树的产量;(2)、如果果园橙子的总产量要达到60375个,考虑到既要成本低,又要保证树与树间的距离不能过密,那么应该多种多少棵橙子树;(3)、增种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?24. 如图,已知双曲线 ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.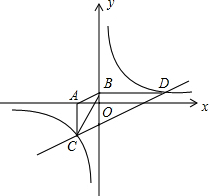 (1)、求k的值;(2)、若△BCD的面积为12,求直线CD的解析式;(3)、判断AB与CD的位置关系,并说明理由.25. 已知锐角△ABC中,边BC长为12,高AD长为8(1)、如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K
(1)、求k的值;(2)、若△BCD的面积为12,求直线CD的解析式;(3)、判断AB与CD的位置关系,并说明理由.25. 已知锐角△ABC中,边BC长为12,高AD长为8(1)、如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K
①求 的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)、若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.