辽宁省沈阳市铁西区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
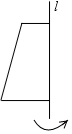 A、
A、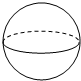 B、
B、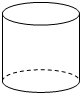 C、
C、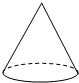 D、
D、 2. 为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是( )
2. 为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是( )
A、企业男员工 B、企业年满50岁及以上的员工 C、用企业人员名册,随机抽取三分之一的员工 D、企业新进员工3. 下列各组数中,互为相反数的是( )A、 B、 C、 D、4. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,点O为直线AB上一点,∠BOC= 则AOC的度数为( )
5. 如图,点O为直线AB上一点,∠BOC= 则AOC的度数为( ) A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误的是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误的是( ) A、 1月份销售为2.2万辆 B、从2月到3月的月销售增长最快 C、4月份销售比3月份增加了1万辆 D、1~4月新能源乘用车销售逐月增加8. 下列各式变形错误的是( )A、 变形为 B、 ,变形为 C、 ,变形为 D、 ,变形为9. 如图,C是AB的中点,D是BC的中点,下列等式不正确的是( )
A、 1月份销售为2.2万辆 B、从2月到3月的月销售增长最快 C、4月份销售比3月份增加了1万辆 D、1~4月新能源乘用车销售逐月增加8. 下列各式变形错误的是( )A、 变形为 B、 ,变形为 C、 ,变形为 D、 ,变形为9. 如图,C是AB的中点,D是BC的中点,下列等式不正确的是( ) A、 B、 C、 D、10. 由若干个完全相同的小立方块搭成一个几何体,这个几何体从左面和上面看到的形状如图所示,则小立方块的个数不可能是( )
A、 B、 C、 D、10. 由若干个完全相同的小立方块搭成一个几何体,这个几何体从左面和上面看到的形状如图所示,则小立方块的个数不可能是( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
11. 计算: .12. 若a,b互为相反数,则a2﹣b2= .13. 如图,将长方形纸片沿AC折叠,使点B落在点 处,CF平分 则∠ACF的度数为.
 14. 在扇形统计图中,其中一个扇形的圆心角是216°,则这部分扇形所表示的部分占总体的百分数是 .
14. 在扇形统计图中,其中一个扇形的圆心角是216°,则这部分扇形所表示的部分占总体的百分数是 .
15. 有理数 在数轴上对应点的位置如图所示,下列结论: 中正确的是(填序号即可). 16. 如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第5个台阶上依次标着 任意相邻四个台阶上数的和都相等,则 .
16. 如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第5个台阶上依次标着 任意相邻四个台阶上数的和都相等,则 .
三、解答题
-
17. 化简:18. 解方程:x- =2- .19. A、B两地相距240千米,一辆公交车从A地出发,以每小时48千米的速度驶向B地;一辆小轿从B地出发,以每小时72千米的速度沿同条道路驶向A地。若小轿车从B地出发1小时后,公交车从A地出发,两车相向而行,求公交车出发后几小时两车相遇?20. 如图,点C、D在线段AB上,若CB=5cm,DB=9m,且点D是AC的中点,求线段AB的长.
 21. 已知A、B是关于 的整式,其中(1)、化简:A+2B;(2)、当 时,A+2B的值为-5,求式子 的值.22. 学校准备添置一批课桌椅,原计划订购60套,每套100元,店方表示:如果多购,可以优惠.结果校方实际订购了72套,每套减价3元,但商店获得了同样多的利润.
21. 已知A、B是关于 的整式,其中(1)、化简:A+2B;(2)、当 时,A+2B的值为-5,求式子 的值.22. 学校准备添置一批课桌椅,原计划订购60套,每套100元,店方表示:如果多购,可以优惠.结果校方实际订购了72套,每套减价3元,但商店获得了同样多的利润.
(1)、求每套课桌椅的成本;(2)、求商店获得的利润.23. 某校为了解七年级学生体育课足球运球的掌握情况,随机抽取部分七年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如图所示的不完整的统计图(说明:A等级:8分~10分;B等级:7分~7.9分;C等级:6分~6.9分;D等级:1分~5.9分):
根据所给信息,解答以下问题:
(1)、在扇形统计图中,求等级C对应的扇形圆心角的度数,并补全条形统计图;(2)、该校七年级有300名学生,请估计足球运球测试成绩达到A等级的学生有多少人?24. 我们知道,分数 可以写成无限循环小数的形式,即 ;反之,无限循环小数 也可以写成分数形式,即 = 事实上,任何无限循环小数都可以写成分数形式.例:无限循环小数 写成分数形式为 方法步骤如下:解:∵ =0.777……
设 则
②-①得
∴ =
同理可得 = =1+ =
根据以上阅读,解答下列问题:
(1)、 = , =;(2)、用题中所给的方法比较 与8的大小: 8(填“>”、“<”或“=”).(3)、将 写成分数形式,请写出解答过程;(4)、将 写成分数形式,请直接写出结果.25. 已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF. (1)、如图1,∠EOF在直线CD的右侧:
(1)、如图1,∠EOF在直线CD的右侧:①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)、如图2,∠EOF在直线CD的左侧,且点E在点F的下方:①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.