广东省佛山市南海区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 已知3x=2y,则x,y一定满足( )A、 , B、 , C、 D、2. 如图,△ABC中,∠C=90°,若AC=4,BC=3,则cosB等于( )
 A、 B、 C、 D、3. 如图,这是由5个大小相同的整体搭成的几何体,该几何体的左视图是 ( )
A、 B、 C、 D、3. 如图,这是由5个大小相同的整体搭成的几何体,该几何体的左视图是 ( ) A、
A、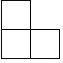 B、
B、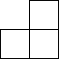 C、
C、 D、
D、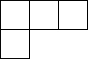 4. 在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有( )A、12个 B、14个 C、18个 D、28个5. 已知a是方程x2-2x-1=0的一个根,则代数式2a2-4a-1的值为( )A、1 B、 C、 或1 D、26. 如图,在△ABC中,DE∥BC,AD=4,AE=3,CE=6,那么BD的值是( )
4. 在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有( )A、12个 B、14个 C、18个 D、28个5. 已知a是方程x2-2x-1=0的一个根,则代数式2a2-4a-1的值为( )A、1 B、 C、 或1 D、26. 如图,在△ABC中,DE∥BC,AD=4,AE=3,CE=6,那么BD的值是( ) A、4 B、6 C、8 D、127. 关于x的一元二次方程9x2-6x+k=0有两个不相等的实根,则k的范围是( )A、 B、 C、 D、8. 如图,丝带重叠的部分一定是( )
A、4 B、6 C、8 D、127. 关于x的一元二次方程9x2-6x+k=0有两个不相等的实根,则k的范围是( )A、 B、 C、 D、8. 如图,丝带重叠的部分一定是( ) A、正方形 B、矩形 C、菱形 D、都有可能9. 已知反比例函数y=﹣ ,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A、正方形 B、矩形 C、菱形 D、都有可能9. 已知反比例函数y=﹣ ,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A、3 B、2 C、1 D、010. 函数y= 与y=-kx+k(k≠0)在同一平面直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离为9m,则AB与CD间的距离是m.
 12. 若两个相似三角形的面积比为1∶4,则这两个相似三角形的周长比是 .13. 如图,点P在反比例函数y= (x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k= .
12. 若两个相似三角形的面积比为1∶4,则这两个相似三角形的周长比是 .13. 如图,点P在反比例函数y= (x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k= . 14. 如图,现有测试距离为5m的一张视力表,表上一个E的高AB为2cm,要制作测试距离为3m的视力表,其对应位置的E的高CD为cm.
14. 如图,现有测试距离为5m的一张视力表,表上一个E的高AB为2cm,要制作测试距离为3m的视力表,其对应位置的E的高CD为cm. 15. 如图,正方形ABCD顶点C、D在反比例函数y= (x>0)图象上,顶点A、B分别在x轴、y轴的正半轴上,则点C的坐标为.
15. 如图,正方形ABCD顶点C、D在反比例函数y= (x>0)图象上,顶点A、B分别在x轴、y轴的正半轴上,则点C的坐标为.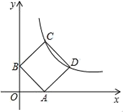
三、解答题
-
16. 计算:2cos60°+tan45°.17. 解方程:x2+4x-3=0.18. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
 (1)、求证:四边形ABCD是矩形;(2)、若AB=2,∠AOB=60°,求BC的长.19. 如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)、求证:四边形ABCD是矩形;(2)、若AB=2,∠AOB=60°,求BC的长.19. 如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°. (1)、如果A、B两楼相距16 米,那么A楼落在B楼上的影子有多长?(2)、如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)20. 有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).(1)、请用表格或树状图列出点A所有可能的坐标;(2)、求点A在反比例函数y= 图象上的概率.21. “低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2014年起逐月增加,据统计,2014年该商城1月份销售自行车64辆,3月份销售了100辆.(1)、求1月到3月自行车销量的月平均增长率;(2)、若按照(1)中自行车销量的增长速度,问该商城4月份能卖出多少辆自行车?22. 如图,点D,E在线段BC上,△ADE是等边三角形,且∠BAC=120°
(1)、如果A、B两楼相距16 米,那么A楼落在B楼上的影子有多长?(2)、如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)20. 有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).(1)、请用表格或树状图列出点A所有可能的坐标;(2)、求点A在反比例函数y= 图象上的概率.21. “低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2014年起逐月增加,据统计,2014年该商城1月份销售自行车64辆,3月份销售了100辆.(1)、求1月到3月自行车销量的月平均增长率;(2)、若按照(1)中自行车销量的增长速度,问该商城4月份能卖出多少辆自行车?22. 如图,点D,E在线段BC上,△ADE是等边三角形,且∠BAC=120° (1)、求证:△ABD∽△CAE;(2)、若BD=2,CE=8,求BC的长.23. 如图,一次函数y=kx+b的图象交反比例函数y= (x>0)的图象于A(4,-8)、B(m,-2)两点,交x轴于点C.
(1)、求证:△ABD∽△CAE;(2)、若BD=2,CE=8,求BC的长.23. 如图,一次函数y=kx+b的图象交反比例函数y= (x>0)的图象于A(4,-8)、B(m,-2)两点,交x轴于点C. (1)、求反比例函数与一次函数的关系式;(2)、根据图象回答:当x为何值时,一次函数的值大于反比例函数的值?(3)、以O、A、B、P为顶点作平行四边形,请直接写出点P的坐标.24. 如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上的动点,且DE=CF,连接DF、AE,AE的延长线交DF于点M,连接OM.
(1)、求反比例函数与一次函数的关系式;(2)、根据图象回答:当x为何值时,一次函数的值大于反比例函数的值?(3)、以O、A、B、P为顶点作平行四边形,请直接写出点P的坐标.24. 如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上的动点,且DE=CF,连接DF、AE,AE的延长线交DF于点M,连接OM. (1)、求证:△ADE≌△DCF;(2)、求证:AM⊥DF;(3)、当CD=AF时,试判断△MOF的形状,并说明理由.25. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒1cm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)、求证:△ADE≌△DCF;(2)、求证:AM⊥DF;(3)、当CD=AF时,试判断△MOF的形状,并说明理由.25. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒1cm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.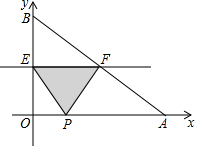 (1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.
(1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.