广东省东莞市2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 方程x2=2x的解是( )A、x=2 B、x=0 C、x1=2,x2=0 D、x1= ,x2=02. 下面数学符号,既是轴对称图形,又是中心对称图形的是( )A、
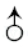 B、
B、 C、
C、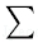 D、
D、 3. a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣ 的图象上,则( )A、a<b<0 B、b<a<0 C、a<0<b D、b<0<a4. 在平面直角坐标系中,点A(6,﹣7)关于原点对称的点的坐标为( )A、(﹣6,﹣7) B、(6,7) C、(﹣6,7) D、(6,﹣7)5. 从 ,0,π, ,6这五个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、6. 反比例函数y=﹣ (x<0)如图所示,则矩形OAPB的面积是( )
3. a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣ 的图象上,则( )A、a<b<0 B、b<a<0 C、a<0<b D、b<0<a4. 在平面直角坐标系中,点A(6,﹣7)关于原点对称的点的坐标为( )A、(﹣6,﹣7) B、(6,7) C、(﹣6,7) D、(6,﹣7)5. 从 ,0,π, ,6这五个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、6. 反比例函数y=﹣ (x<0)如图所示,则矩形OAPB的面积是( ) A、3 B、﹣3 C、 D、﹣7. 如图,在△ABC中,DE∥BC , 分别交AB , AC于点D , E . 若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
A、3 B、﹣3 C、 D、﹣7. 如图,在△ABC中,DE∥BC , 分别交AB , AC于点D , E . 若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( ) A、 B、 C、 D、8. 如图,⊙O的直径AB垂直于弦CD , ∠CAB=36°,则∠BCD的大小是( )
A、 B、 C、 D、8. 如图,⊙O的直径AB垂直于弦CD , ∠CAB=36°,则∠BCD的大小是( ) A、18° B、36° C、54° D、72°9. 若关于x的一元二次方程x2﹣2x+m=0没有实数根,则实数m的取值是( )A、m<1 B、m>﹣1 C、m>1 D、m<﹣110. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )A、
A、18° B、36° C、54° D、72°9. 若关于x的一元二次方程x2﹣2x+m=0没有实数根,则实数m的取值是( )A、m<1 B、m>﹣1 C、m>1 D、m<﹣110. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )A、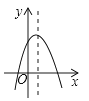 B、
B、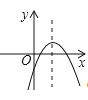 C、
C、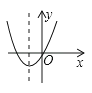 D、
D、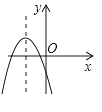
二、填空题
-
11. 反比例函数y= 经过点(2,3),则k= .12. 二次函数y=4(x﹣3)2+7的图象的顶点坐标是 .13. 在一个不透明的口袋中,装有4个红球和若干个白球,这些球除颜色外其余都相同,如果摸到红球的概率是 ,那么口袋中有白球个14. m是方程x2+x﹣1=0的根,则式子m2+m+2018的值为 .15. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为米.
 16. 如图,AB与⊙O相切于点B , AO的延长线交⊙O于点C , 连接BC , 若∠ABC=120°,OC=3,则弧BC的长为(结果保留π).
16. 如图,AB与⊙O相切于点B , AO的延长线交⊙O于点C , 连接BC , 若∠ABC=120°,OC=3,则弧BC的长为(结果保留π).
三、解答题
-
17. 解方程:3(x﹣4)2=﹣2(x﹣4)18. 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
 (1)、△ABP旋转的旋转中心是什么?旋转了多少度?(2)、若BP=2,求PE的长.19. 袋中有一个红球和两个自球,它们除颜色外其余都相同,任意摸出一球,记下球的颜色,放回袋中,搅匀后再任意摸出一球,记下它的颜色.
(1)、△ABP旋转的旋转中心是什么?旋转了多少度?(2)、若BP=2,求PE的长.19. 袋中有一个红球和两个自球,它们除颜色外其余都相同,任意摸出一球,记下球的颜色,放回袋中,搅匀后再任意摸出一球,记下它的颜色. (1)、请把树状图填写完整.(2)、根据树状图求出两次都摸到白球的概率.20. 如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于E , 交AC延长线于F .
(1)、请把树状图填写完整.(2)、根据树状图求出两次都摸到白球的概率.20. 如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于E , 交AC延长线于F .
求证:
(1)、△ADF∽△EDB;(2)、CD2=DE•DF .21. 如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上. (1)、将△ABC绕点O顺时针旋转90°后,得到△A1B1C1 . 在网格中画出△A1B1C1;(2)、求线段OA在旋转过程中扫过的图形面积;(结果保留π)22. 受益于国家支持新能源汽车发展和“一带一路”倡议,某市汽车零部件生产企业的利润逐年提高,据统计,2017年的利润为2亿元,2019 年的利润为2.88亿元.(1)、求该企业从2017年到2019年年利润的平均增长率?(2)、若年利润的平均增长率不变,则该企业2020年的利润能后超过3.5亿元?23. 如图,直线y=2x与反比例函数y= (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B .
(1)、将△ABC绕点O顺时针旋转90°后,得到△A1B1C1 . 在网格中画出△A1B1C1;(2)、求线段OA在旋转过程中扫过的图形面积;(结果保留π)22. 受益于国家支持新能源汽车发展和“一带一路”倡议,某市汽车零部件生产企业的利润逐年提高,据统计,2017年的利润为2亿元,2019 年的利润为2.88亿元.(1)、求该企业从2017年到2019年年利润的平均增长率?(2)、若年利润的平均增长率不变,则该企业2020年的利润能后超过3.5亿元?23. 如图,直线y=2x与反比例函数y= (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B . (1)、求k的值;(2)、点C在AB上,若OC=AC , 求AC的长;(3)、点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD , 求点D的坐标.
(1)、求k的值;(2)、点C在AB上,若OC=AC , 求AC的长;(3)、点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD , 求点D的坐标.

