广东省珠海市香洲区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段，能组成三角形的是（）

A、3，4，8 B、6，7，8 C、5，6，11 D、1，4，7

查看试题解析
3. 点A（2，﹣1）关于x轴对称的点B的坐标为（）

A、（2，1） B、（﹣2，1） C、（2，﹣1） D、（﹣2，﹣1）

查看试题解析
4. 若分式 $\frac{1}{x + 1}$ 有意义，则x的取值范围是（）

A、x≠0 B、x≠1 C、x≠﹣1 D、x取任意实数

查看试题解析
5. 下列计算正确的是（）

A、a²+a³＝a⁵ B、（a²）³＝a⁶ C、a⁶÷a²＝a³ D、2a×3a＝6a

查看试题解析
6. 如图，AB＝CD ， AE⊥BC ， DF⊥BC ，垂足分别为E ， F ， CE＝BF ，下列结论错误的是（）

A、∠C＝∠B B、DF∥AE C、∠A+∠D＝90° D、CF＝BE

查看试题解析
7. 下列多项式能用完全平方公式进行因式分解的是（）

A、a²﹣1 B、a²+4 C、a²+2a+1 D、a²﹣4a﹣4

查看试题解析
8. 如果把分式 $\frac{2 x}{3 x - 2 y}$ 中的x，y都扩大3倍，那么分式的值 $($ $)$

A、扩大3倍 B、不变 C、缩小3倍 D、扩大2倍

查看试题解析
9. 如图，在△ABC中，∠B＝50°，∠A＝30°，CD平分∠ACB ， CE⊥AB于点E ，则∠DCE的度数是（）

A、5° B、8° C、10° D、15°

查看试题解析
10. 如图，设k＝ $\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$ （a＞b＞0），则有（）

A、0＜k＜ $\frac{1}{2}$ B、 $\frac{1}{2}$ ＜k＜1 C、0＜k＜1 D、1＜k＜2

查看试题解析

二、填空题

11. 2^﹣¹等于．

查看试题解析
12. 如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为.

查看试题解析
13. 因式分解：a²﹣2a= ．

查看试题解析
14. 如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，则∠DBC＝度．

查看试题解析
15. 已知（x+y）²＝25，（x﹣y）²＝9，则x²+y²＝．

查看试题解析
16. 如图，等边△ABC的周长为18cm ， BD为AC边上的中线，动点P ， Q分别在线段BC ， BD上运动，连接CQ ， PQ ，当BP长为cm时，线段CQ+PQ的和为最小．

查看试题解析

三、解答题

17. 计算：（2x+y）（2x﹣y）+y（2x+y）．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°．

(1)、尺规作图：作∠B的平分线BD交AC于点D；（不写作法，保留作图痕迹）

(2)、若DC＝2，求AC的长．

查看试题解析
19. 解方程： $\frac{x}{x - 2} + \frac{2}{x} = 1$ ．

查看试题解析
20. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ÷（ $\frac{x}{x + 1}$ ﹣1），其中x＝﹣2018．

查看试题解析
21. 如图，在△ABC中，点D在BC上，AB＝AC＝BD ， AD＝DC ，将△ACD沿AD折叠至△AED ， AE交BC于点F ．

(1)、求∠C的度数；

(2)、求证：BF＝CD ．

查看试题解析
22. 港珠澳大桥是世界最长的跨海大桥，连接香港大屿山、澳门半岛和广东省珠海市，其中珠海站到香港站全长约55千米，2018年10月24日上午9时正式通车．一辆观光巴士自珠海站出发，25分钟后，一辆小汽车从同一地点出发，结果同时到达香港站．已知小汽车的速度是观光巴士的1.6倍，求观光巴士的速度．

查看试题解析
23. 观察下列式子：
0×2+1＝1²……①

1×3+1＝2²……②

2×4+1＝3²……③

3×5+1＝4²……④

……

(1)、第⑤个式子，第⑩个式子；

(2)、请用含n（n为正整数）的式子表示上述的规律，并证明：

(3)、求值：（1+ $\frac{1}{1 \times 3}$ ）（1+ $\frac{1}{2 \times 4}$ ）（1+ $\frac{1}{3 \times 5}$ ）（1+ $\frac{1}{4 \times 6}$ ）…（1+ $\frac{1}{2016 \times 2018}$ ）．

查看试题解析
24. 如图，在等腰△ABC中，AB＝AC ，过点B作BD⊥AB ，过点C作CD⊥BC ，两线相交于点D ， AF平分∠BAC交BC于点E ，交BD于点F ．

(1)、若∠BAC＝68°，求∠DBC；

(2)、求证：点F为BD中点；

(3)、若AC＝BD ，且CD＝3，求四边形ABDC的面积．

查看试题解析
25. 如图，在Rt△ABO中，∠BAO＝90°，AO＝AB，BO＝8 $\sqrt{2}$ ，点A的坐标（﹣8，0），点C在线段AO上以每秒2个单位长度的速度由A向O运动，运动时间为t秒，连接BC，过点A作AD⊥BC，垂足为点E，分别交BO于点F，交y轴于点 D.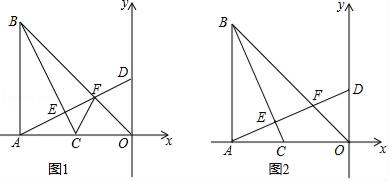

(1)、用t表示点D的坐标；

(2)、如图1，连接CF，当t＝2时，求证：∠FCO＝∠BCA；

(3)、如图2，当BC平分∠ABO时，求t的值.

查看试题解析