广东省深圳市南山区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、 $3.14$ B、 $\sqrt[3]{8}$ C、 $\sqrt{15}$ D、 $\sqrt{16}$

查看试题解析
2. 在下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{12}$ D、 $\sqrt{27}$

查看试题解析
3. 点P（-2，-3）关于x轴的对称点为（）

A、 $(- 3, - 2)$ B、 $(2, 3)$ C、 $(2, - 3)$ D、 $(- 2, 3)$

查看试题解析
4. 一组数据由m个a和n个b组成，那么这组数据的平均数是（）

A、 $\frac{a + b}{2}$ B、 $\frac{a + b}{m + n}$ C、 $\frac{m a + n b}{a + b}$ D、 $\frac{m a + n b}{m + n}$

查看试题解析
5. 已知点A（m+1，-2）和点B（3，m-1），若直线AB∥x轴，则m的值为（）

A、 $- 1$ B、 $- 4$ C、2 D、3

查看试题解析
6. 某一次函数的图象经过点（1，2），且y随x的增大而减小，则这个函数的表达式可能是（）

A、 $y = 2 x + 4$ B、 $y = 3 x - 1$ C、 $y = - 3 x + 1$ D、 $y = - 2 x + 4$

查看试题解析
7. 以方程组 ${\begin{matrix} y = - x + 2 \\ y = x - 1 \end{matrix}$ 的解为坐标的点（x，y）在平面直角坐标系中的位置是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图是某单元楼居民六月份的用电(单位：度)情况，则关于用电量的描述错误的是（）

A、众数为30 B、中位数为25 C、平均数为24 D、方差为83

查看试题解析
9. 如图所示，b∥c，a⊥b，∠1=130°，则∠2=（）．

A、30° B、40° C、50° D、60°

查看试题解析
10. 如图是一次函数y₁=kx+b与y₂=x+a的图象，则下列结论：①k＜0；②a＞0；③b＞0：④方程kx+b=x+a的解是x=3，错误的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用 $x$ ， $y$ 表示直角三角形的两直角边 $(x > y)$ ，下列四个说法：① $x^{2} + y^{2} = 49$ ；② $x - y = 2$ ；③ $x + y = \sqrt{94}$ ；④ $2 x y + 4 = 49$ ；其中说法正确的是 $($ $)$

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

12. 64的平方根是.

查看试题解析
13. 一组数据：﹣1，3，2，x，5，它有唯一的众数是3，则这组数据的中位数是．

查看试题解析
14. 如图，一个正比例函数图象与一次函数y=-x+1的图像相交于点P，则这个正比例函数的表达式是

查看试题解析
15. 如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是．

查看试题解析

三、解答题

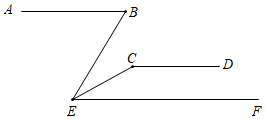
16. 解下列方程组

(1)、 ${\begin{matrix} x + 2 y = 0 \\ 3 x + 4 y = 6 \end{matrix}$

(2)、 ${\begin{array}{l} \frac{y + 1}{4} = \frac{x + 2}{3} \\ 2 x - 3 y = 1 \end{array}$

查看试题解析
17. 计算

(1)、2 $\sqrt{2}$ -2 $\sqrt{3}$ +3 $\sqrt{2} + 3 \sqrt{3}$

(2)、（ $\sqrt{7} + \sqrt{3}$ ）（ $\sqrt{7} - \sqrt{3}$ ）

(3)、 $\frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}}$ + $\sqrt[3]{- 8}$

(4)、 $\sqrt{{(- 5)}^{2}}$ +|3- $\sqrt{12}$ |- $\frac{6}{\sqrt{3}}$ +（ $\frac{1}{3}$ ）^-1

查看试题解析
18. 如图，AB∥CD∥EF ，且∠ABE=70°，∠ECD=150°，求∠BEC的度数．

查看试题解析
19. 如图，在四边形ABDC中，∠A=90°，AB=9，AC=12，BD=8，CD=17．

(1)、连接BC ，求BC的长；

(2)、求△BCD的面积．

查看试题解析
20. 某校为奖励该校在南山区第二届学生技能大赛中表现突出的20名同学，派李老师为这些同学购买奖品，要求每人一件，李老师到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．

(1)、求笔记本和钢笔的单价分别为多少元？

(2)、售货员提示，购买笔记本没有优惠：买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞10）支钢笔，所需费用为y元，请你求出y与x之间的函数关系式；

(3)、在（2）的条件下，如果买同一种奖品，请你帮忙计算说明，买哪种奖品费用更低．

查看试题解析
21. 对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），
则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．

(1)、点P（﹣2，3）的“3属派生点”P′的坐标为；

(2)、若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；

(3)、若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

查看试题解析
22. 如图，在平面直角坐标系xOy中，直线y＝﹣ $\frac{4}{3}$ x+4与x轴、y轴分别交于点A、点B ，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．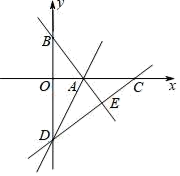

(1)、求AB的长；

(2)、求点C和点D的坐标；

(3)、y轴上是否存在一点P ，使得S_△_PAB＝ $\frac{1}{2}$ S_△_OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析