广东省深圳市宝安区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是 $($ $)$

A、 $\sqrt{4}$ B、 $\sqrt[3]{- 27}$ C、 $\frac{24}{7}$ D、 $\sqrt{3}$

查看试题解析
2. 已知点P位于第二象限，则点P的坐标可能是 $($ $)$

A、 $(- 3 ， 0)$ B、 $(0 ， 3)$ C、 $(- 3 ， 2)$ D、 $(- 3 ， - 3)$

查看试题解析
3. 下列计算正确的是 $($ $)$

A、 $\sqrt{18} \div \sqrt{3} = 6$ B、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{{(- 5)}^{2}} = - 5$

查看试题解析
4. 已知二元一次方程组 ${\begin{array}{l} \overset{ax - y + b = 0}{kx - y = 0} \end{array}$ 的解为 ${\begin{array}{l} \overset{x = - 3}{y = 1} \end{array}$ ，则函数 $y = ax + b$ 和 $y = kx$ 的图象交点为坐标为 $($ $)$

A、 $(3 ， - 1)$ B、 $(- 3 ， 1)$ C、 $(1 ， - 3)$ D、 $(- 1 ， 3)$

查看试题解析
5. 如图1，将三角板的直角顶点放在直角尺的一边上，∠1=30°，∠2=50°，则∠3的度数为（）

A、80° B、50° C、30° D、20°

查看试题解析
6. 某车间需加工一批零件，车间20名工人每天加工零件数如表所示：

每天加工零件数

4

5

6

7

8

人数

3

6

5

4

2

每天加工零件数的中位数和众数为（　　）

A、6，5 B、6，6 C、5，5 D、5，6

查看试题解析
7. 如图，将一根长为8cm（AB=8cm）的橡皮筋水平放置在桌面上，固定两端A和B，然后把中点C竖直地向上拉升3cm至D点，则拉长后橡皮筋的长度为（）

A、8cm B、10cm C、12.cm D、15cm

查看试题解析
8. 下列命题中，真命题的是 $($ $)$

A、同旁内角互补 B、相等的角是对顶角 C、同位角相等，两直线平行 D、直角三角形两个锐角互补

查看试题解析
9. 为丰富同学们的课余活动，某校计划成立足球和篮球课外兴趣小组，现需购买篮球和足球若干个，已知购买篮球的数量比足球的数量少1个，篮球的单价为60元，足球的单价为30元，一共花了480元，问篮球和足球各买了多少个？设购买篮球x个，购买足球y个，可列方程组 $($ $)$

A、 ${\begin{matrix} x - y = 1 \\ 60 x + 30 y = 480 \end{matrix}$ B、 ${\begin{matrix} x=y- 1 \\ 60 x + 30 y = 480 \end{matrix}$ C、 ${\begin{matrix} x=y- 1 \\ 30 x + 60 y = 480 \end{matrix}$ D、 ${\begin{matrix} x-y= 1 \\ 30 x + 60 y = 480 \end{matrix}$

查看试题解析
10. 如图，小巷左右两侧是竖直的墙壁，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为 $0.7$ 米，顶端距离地面 $2.4$ 米 $.$ 若梯子底端位置保持不动，将梯子斜靠在右墙时，顶端距离地面 $1.5$ 米，则小巷的宽度为 $($ $)$

A、 $2.7$ 米 B、 $2.5$ 米 C、2米 D、 $1.8$ 米

查看试题解析
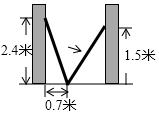11. 在平面直角坐标系中，经过二、三、四象限的直线l过点 $(- 3 ， - 2) .$ 点 $(- 2 ， a)$ ， $(0 ， b)$ ， $(c ， 1)$ ， $(d ， - 1)$ 都在直线l上，则下列判断正确的是 $($ $)$

A、 $a = - 3$ B、 $b > - 2$ C、 $c < - 3$ D、 $d = - 2$

查看试题解析
12. 某商店有一款畅销服装原价为40元，该商店规定：若顾客购买服装数量在20件以内，则按原价进行销售：若顾客购买服装数量超过20件，超过的部分每件可以享受指定的折扣，现八 $(2)$ 班同学为参加学校秋季运动会，准备统一向该商店购买该款服装，所需费用 $y ($ 元 $)$ 与购买数量 $x ($ 件 $)$ 之间的函数关系如图所示，那么购买数量超过20件的部分每件享受到的折扣是 $($ $)$

A、9折 B、8折 C、 $7.5$ 折 D、7折

查看试题解析

二、填空题

13. 8的立方根是．

查看试题解析
14. 小林同学对甲、乙、丙三个市场某月份每天的白菜价格进行调查，计算后发现这个月三个市场的价格平均值相同，方差分别为S_甲²＝7.5，S_乙²＝1.5，S_丙²＝3.1，那么该月份白菜价格最稳定的是市场．

查看试题解析
15. 如图，在 $△ ABC$ 中， $∠ ABC$ 的平分线与 $∠ ACB$ 的平分线交于点D，过点D作BC的平行线交AB于点E，交AC于点F，已知 $∠ BED + ∠ CFD = 240^{\circ}$ ，则 $∠ BDC =$ ．

查看试题解析
16. 如图，直线 $y = \frac{4}{3} x + 4$ 交x轴于点A，交y轴于点B，点C为线段OB上一点，将 $△ ABC$ 沿着直线AC翻折，点B恰好落在x轴上的D处，则 $△ ACD$ 的面积为．

查看试题解析

三、解答题

17. 解方程

(1)、 ${\begin{array}{l} 5 x + y = 4 \\ x = 3 y + 4 \end{array}$

(2)、 ${\begin{array}{l} 2 x - y = 5 \\ 7 x - 3 y = 20 \end{array}$ .

查看试题解析
18. 计算：

(1)、 $\sqrt{8} (\sqrt{2} - 1) + \sqrt{18}$

(2)、 $\frac{\sqrt{12} + \sqrt{3}}{\sqrt{3}} - \sqrt{\frac{2}{3}} \times \sqrt{24}$

查看试题解析
19. 八年级（1）班的同学积极响应学校团委号召，每位同学都向“希望工程”捐献图书 $.$ 全班捐书情况如图，请你根据图中提供的信息解答以下问题：

(1)、该班共有名学生；

(2)、将条形统计图补充完整；

(3)、该班同学平均每人捐书册 $.$

查看试题解析
20. 如图，在 $△ ABC$ 中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得 $EF = ED$ ，连CF．

(1)、求证： $CF / / AB$

(2)、若 $∠ ABC = 50^{\circ}$ ，连接BE，BE平分 $∠ ABC$ ，AC平分 $∠ BCF$ ，求 $∠ A$ 的度数．

查看试题解析
21. 某班师生共44人去公园划船，公园有大、小两种型号的船只，每艘船可容纳的人数和费用如下表：

大船
小船
每艘船可容纳人数
8
5
每艘船的费用
200
150
若每艘船刚好坐满（即没有空位），一共花费1200元 $.$ 请问公园提供了大、小船各多少艘？

查看试题解析
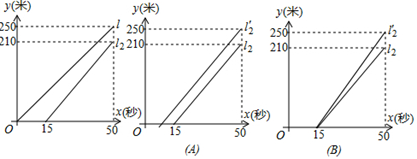
22. 小华和小峰是两名自行车爱好者，小华的骑行速度比小峰快 $.$ 两人准备在周长为250米的赛道上进行一场比赛 $.$ 若小华在小峰出发15秒之后再出发，图中 $l_{1}$ 、 $l_{2}$ 分别表示两人骑行路程与时间的关系．

(1)、小峰的速度为米 $/$ 秒，他出发米后，小华才出发；

(2)、小华为了能和小峰同时到达终点，设计了两个方案，方案一：加快骑行速度；方案二：比预定时间提前出发．
①图 $($ 填“A“”或“B“ $)$ 代表方案一；

②若采用方案二，小华必须在小峰出发多久后开始骑行？求出此时小华骑行的路程与时间的函数关系式．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x - 3$ 交x轴于点A，交y轴于点B，交直线 $x = a$ 于点C，点D与点B关于x轴对称，连接AD交直线 $x = a$ 于点E．

(1)、填空： $S_{△ ABD} =$ ．

(2)、求直线AD的解析式；

(3)、在x轴上存在一点P，则 $PE + PD$ 的和最小为； $($ 直接填空即可 $)$

(4)、当 $- 4 < a < 0$ 时，点Q为y轴上的一个动点，使得 $△ QEC$ 为等腰直角三角形，求点Q的坐标．

查看试题解析

	大船	小船
每艘船可容纳人数	8	5
每艘船的费用	200	150

每天加工零件数	4	5	6	7	8
人数	3	6	5	4	2