湖北省武汉市新洲区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 某种食品保存的温度是﹣10±2℃，以下几个温度中，不适合储存这种食品的是（　　）

A、﹣6℃ B、﹣8℃ C、﹣10℃ D、﹣12℃

查看试题解析
2. 下列各式中，不相等的是（　　）

A、（﹣2）²和2² B、|﹣2|³和|﹣2³| C、（﹣2）²和﹣2² D、（﹣2）³和﹣2³

查看试题解析
3. 港珠澳大桥2018年10月24日上午9时正式通车，这座大桥跨越伶仃洋，东接香港，西接广东珠海和澳门，总长约55000m，集桥、岛、隧于一体，是世界最长的跨海大桥，数据55000用科学记数法表示为（）

A、5.5×10⁵ B、55×10⁴ C、5.5×10⁴ D、5.5×10⁶

查看试题解析
4. 若单项式3x^m+1y⁴与﹣ $\frac{2}{3}$ x²y⁴^﹣³ⁿ是同类项，则m $\cdot$ n的值为（　　）

A、2 B、1 C、﹣1 D、0

查看试题解析
5. 下列运算中，正确的是（）．

A、 $3 a + 2 b = 5 a b$ B、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ C、 $3 a^{2} b - 3 b a^{2} = 0$ D、 $5 a^{2} - 4 a^{2} = 1$

查看试题解析
6. 如图是一个正方体的展开图，则“数”字的对面的字是 $($ $)$

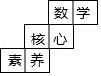A、核 B、心 C、素 D、养

查看试题解析
7. 如图，甲从A点出发向北偏东60°方向走到点B，乙从点A出发向南偏西20°方向走到点C，则∠BAC的度数是（）

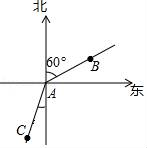A、80° B、100° C、120° D、140°

查看试题解析
8. 如图，是由相同的花盆按一定的规律组成的形如正多边形的图案，其中第1个图形共有6个花盆，第2个图形一共有12个花盆，第3个图形一共有20个花盆，…，则第10个图形中花盆的个数为（　　）

A、110 B、120 C、132 D、140

查看试题解析
9. 已知有理数a，b，c，d在数轴上对应的点如图所示，每相邻两个点之间的距离是1个单位长度.若3a＝4b﹣3，则c﹣2d为（）

A、﹣3 B、﹣4 C、﹣5 D、﹣6

查看试题解析
10. 一件工程甲独做50天可完，乙独做75天可完，现在两个人合作，但是中途乙因事离开几天，从开工后40天把这件工程做完，则乙中途离开了（　　）天.

A、10 B、20 C、30 D、25

查看试题解析

二、填空题

11. 计算：﹣6+4＝.

查看试题解析
12. 若（3﹣m）x^|^m^|^﹣²﹣1＝0是关于x的一元一次方程，则m的值为.

查看试题解析
13. 若点A、B是数轴上的两个点，点A表示的数是﹣4，点B与点A的距离是2，点B表示的数是.

查看试题解析
14. 某同学做了一道数学题：“已知两个多项式为 A、B，B=3x﹣2y，求 A﹣B 的值．”他误将“A﹣B”看成了“A+B”，结果求出的答案是 x ﹣y，那么原来的 A﹣B的值应该是．

查看试题解析
15. 如图，延长线段AB至C使BC＝2AB，延长线段BA至D使AD＝3AB，点E是线段DB的中点，点F是线段AC的中点，若EF＝10cm，则AB的长度为cm.

查看试题解析
16. 按下面的程序计算：

如果输入x的值是正整数，输出结果是150，那么满足条件的x的值有个 $.$

查看试题解析

三、解答题

17. 计算:

(1)、2×（﹣5）﹣（﹣3）÷ $\frac{3}{4}$ ；

(2)、﹣4⁴﹣15+（﹣2）³+|﹣ $\frac{1}{2}$ |×（1﹣0.5）

查看试题解析
18. 已知A＝2a²+3ab﹣2a﹣1，B＝﹣a²+ $\frac{1}{2} a b + \frac{2}{3}$

(1)、当a＝﹣1，b＝﹣2时，求4A﹣（3A﹣2B）的值；

(2)、若（1）中式子的值与a的取值无关，求b的值.

查看试题解析
19. 解方程：

(1)、7﹣2x＝3﹣4（x﹣2）

(2)、 $\frac{2 x - 1}{3} = \frac{2 x + 1}{6} - 1$

查看试题解析
20. 已知a、b是有理数，运算“⊕”的定义是：a⊕b＝ab+a﹣b.

(1)、求2⊕（﹣3）的值；

(2)、若x⊕ $\frac{3}{4}$ ＝1求x的值；

(3)、运算“⊕”是否满足交换律，请证明你的结论.

查看试题解析
21. 某水泥厂仓库6天内进出水泥的吨数如下（“+”表示进库，“﹣”表示出库）：+50、﹣45、﹣33、+48、﹣49、﹣36.

(1)、经过这6天，仓库里的水泥是增多还是减少了？增多或减少了多少吨？

(2)、经过这6天，仓库管理员结算发现库里还存200吨水泥，那么6天前，仓库里存有水泥多少吨？

(3)、如果进出仓库的水泥装卸费都是每吨5元，那么这6天要付多少元装卸费.

查看试题解析

22. 节约用水.市政府决定对居民用水实行三级阶梯水价，收费标准如下表：

每户每月用水量	水费价格（单位：元/立方米）
不超过22立方米	2.3
超过22立方米且不超过30立方米的部分	a
超过30立方米的部分	4.6

(1)、若小明家去年1月份用水量是20立方米，他家应缴费元.

(2)、若小明家去年2月份用水量是26立方米，缴费64.4元，请求出用水在22～30立方米之间的收费标准a元/立方米？

(3)、在（2）的条件下，若小明家去年8月份用水量增大，共缴费87.4元，请求出他家8月份的月水量是多少立方米？

查看试题解析

23. 如图，直线MN与直线PQ相交于点O，点A在直线PQ上运动，点B在直线MN上运动.

(1)、如图1，若∠AOB＝80°，AE、BE分别是∠BAO和∠ABO的角平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的理由；若不发生变化，试求出∠AEB的度数；

(2)、如图2，若∠AOB＝90°，点D、C分别是∠PAB和∠ABM的角平分线上的两点，AD、BC交于点F.∠ADC和∠BCD的角平分线相交于点E，
①点AB在运动的过程中，∠F的大小是否会发生变化？若发生变化，请说明变化的理由；若不发生变化，请求其度数.

②点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明变化的理由；若不发生变化，请求其度数.

查看试题解析
24. 定义：若线段上的一个点把这条线段分成1：2的两条线段，则称这个点是这条线段的三等分点.如图1，点C在线段AB上，且AC：CB＝1：2，则点C是线段AB的一个三等分点，显然，一条线段的三等分点有两个.

(1)、已知：如图2，DE＝15cm ，点P是DE的三等分点，求DP的长.

(2)、已知，线段AB＝15cm ，如图3，点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动；点Q从点B出发，先向点A方向运动，当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm ，设运动时间为t秒.
①若点P点Q同时出发，且当点P与点Q重合时，求t的值.

②若点P点Q同时出发，且当点P是线段AQ的三等分点时，求t的值.

查看试题解析