广东省汕头市金平区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是 $($ )

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 ${(x y)}^{2} = x y^{2}$ C、 ${(x^{2})}^{4} = x^{8}$ D、 $x^{2} + x^{3} = x^{5}$

查看试题解析
2. 下列图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列三条线段中，能构成三角形的是（）

A、3，4，8 B、5、6，7 C、5，5，10 D、5，6，11

查看试题解析
4. 下列选项中最简分式是（）

A、 $\frac{1}{x^{2} + 1}$ B、 $\frac{2}{4 x^{2}}$ C、 $\frac{x + 1}{x^{2} - 1}$ D、 $\frac{3 x^{2} + x}{x}$

查看试题解析
5. 下列条件中，能判定△ABC为直角三角形的是（　　）

A、∠A=2∠B=3∠C B、∠A+∠B=2∠C C、∠A=∠B=30° D、∠A= $\frac{1}{2}$ ∠B= $\frac{1}{3}$ ∠C

查看试题解析
6. 如图，△ABC≌△AED，点D在BC上，若∠EAB＝42°，则∠DAC的度数是（）

A、48° B、44° C、42° D、38°

查看试题解析
7. 如图，在△ABC中，∠A＝31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分AB，那么∠C的度数为（）

A、93° B、87° C、91° D、90°

查看试题解析
8. 工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C作射线OC，由做法得△MOC≌△NOC的依据是（）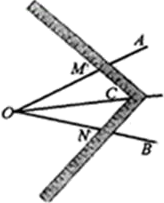

A、AAS B、SAS C、ASA D、SSS

查看试题解析
9. 下列各式中，从左到右的变形是因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} - 4 x + 4 = x (x - 4) + 4$ C、 $(x + 3) (x - 4) = x^{2} - x - 12$ D、 $x^{2} - 4 = (x + 2) (x - 2)$

查看试题解析
10. 对于两个不相等的实数a、b，我们规定符号Min{a ， b}表示a、b中的较小的值，如Min{2，4}＝2，按照这个规定，方程Min{ $\frac{1}{x}$ ， $\frac{2}{x}$ }＝ $\frac{3}{x}$ －1的解为（）

A、1 B、2 C、1或2 D、1或－2

查看试题解析

二、填空题

11. 当x= ，分式 $\frac{x - 2}{x^{2} + 1}$ 的的值为零。

查看试题解析
12. 已知一个三角形的两边长分别为2和5，第三边 $x$ 的取值范围为.

查看试题解析
13. 分式 $\frac{y}{2 x}$ ， $\frac{x}{3 y^{2}}$ ， $\frac{1}{4 x y}$ 的最简公分母是.

查看试题解析
14. 光的速度约为3×10⁵ km/s,太阳系以外距离地球最近的一颗恒星(比邻星)发出的光需要4年的时间才能到达地球.若一年以3×10⁷ s计算,则这颗恒星到地球的距离是km.

查看试题解析
15. 如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是．

查看试题解析
16. 如图，∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂ ， B₃…在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄…均为等边三角形，从左起第1个等边三角形的边长记a₁ ，第2个等边三角形的边长记为a₂ ，以此类推，若OA₁＝3，则a₂= ， a₂₀₁₉=.

查看试题解析

三、解答题

17. 先化简，再求值：(x﹣2y)²﹣x(x+3y)﹣4y² ，其中x＝﹣4，y＝ $\frac{1}{2}$ ．

查看试题解析
18. 一个多边形内角和的度数比外角和的度数的4倍多180度，求多边形的边数。

查看试题解析
19. 如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB＝6，若S_△_ABD＝12，求DF的长.

查看试题解析
20. 先化简再求值： $\frac{x^{2} - 1}{x + 2} \div (1 - \frac{1}{x + 2})$ ，其中x＝ $\frac{1}{3}$

查看试题解析
21. 如图，△ABC中，∠B＝2∠C．

(1)、尺规作图：作AC的垂直平分线，交AC于点D，交BC于点E；

(2)、连接AE，求证：AB＝AE

查看试题解析
22. 山地自行车越来越受中学生的喜爱．一网店经营的一个型号山地自行车，今年一月份销售额为30000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是27000元．

(1)、求二月份每辆车售价是多少元？

(2)、为了促销，三月份每辆车售价比二月份每辆车售价降低了10%销售，网店仍可获利35%，求每辆山地自行车的进价是多少元？

查看试题解析
23. 特殊两位数乘法的速算——如果两个两位数的十位数字相同，个位数字相加为10，那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC（即十位数字为A，个位数字分别为B、C，B+C=10，A>3），那么它们的乘积是一个4位数，前两位数字是A和(A+1)的乘积，后两位数字就是B和C的乘积.
如：47×43=2021，61×69=4209.

(1)、请你直接写出83×87的值；

(2)、设这两个两位数的十位数字为x(x>3)，个位数字分别为y和z（y+z=10)，通过计算验证这两个两位数的乘积为100x(x+1)+yz.

(3)、99991×99999=（直接填结果）

查看试题解析
24. 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD ，作∠ADE=40°，DE交线段AC于E点．

(1)、当∠BDA=115°时，∠BAD=°，∠DEC=°；

(2)、当DC等于多少时，△ABD与△DCE全等？请说明理由；

(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数；若不可以，请说明理由．

查看试题解析
25. 如图1，△ABC是边长为8的等边三角形，AD⊥BC于点D，DE⊥AB于点E.

(1)、求证：AE＝3EB

(2)、若点F是AD的中点，点P是BC边上的动点，连接PE，PF，如图2所示，求PE＋PF的最小值及此时BP的长；

(3)、在（2）的条件下，连接EF，当PE＋PF取最小值时，△PEF的面积是.

查看试题解析