广东省广州市海珠区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案是我国几家银行的标志，其中是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算中，正确的是（）

A、a²•a⁴＝a⁸ B、a¹⁰÷a⁵＝a² C、（a⁵）²＝a¹⁰ D、（2a）⁴＝8a⁴

查看试题解析
3. 下列变形属于因式分解的是（）

A、4x+x＝5x B、（x+2）²＝x²+4x+4 C、x²+x+1＝x（x+1）+1 D、x²﹣3x＝x（x﹣3）

查看试题解析
4. 石墨烯目前是世界上最薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为（）

A、0.34×10^﹣⁹ B、3.4×10^﹣⁹ C、3.4×10^﹣¹⁰ D、3.4×10^﹣¹¹

查看试题解析
5. 已知图中的两个三角形全等，图中的字母表示三角形的边长，则∠1等于（）

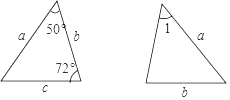A、72° B、60° C、50° D、58°

查看试题解析
6. 如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D ，交AC于点E ，则△BEC的周长为（）

A、13 B、16 C、8 D、10

查看试题解析
7. 下列各式成立的是（）

A、 $\frac{x - 2 y}{2 y - x}$ =1 B、（﹣a﹣b）²＝（a+b）² C、（a﹣b）²＝a²﹣b² D、（a+b）²﹣（a﹣b）²＝2ab

查看试题解析
8. 如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，若添加下列一个条件后，仍然不能证明△ABC≌△DEF，则这个条件是（）

A、∠A＝∠D B、BC＝EF C、∠ACB＝∠F D、AC＝DF

查看试题解析
9. 下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）

A、①②③ B、①②④ C、①③ D、①②③④

查看试题解析
10. 已知x＝3y+5，且x²﹣7xy+9y²＝24，则x²y﹣3xy²的值为（）

A、0 B、1 C、5 D、12

查看试题解析

二、填空题

11. 因式分解：2a²﹣8= ．

查看试题解析
12. 若代数式 $\frac{x - 1}{x - 3}$ 有意义，则实数x的取值范围是．

查看试题解析
13. 一个n边形的内角和是540°，那么n= ．

查看试题解析
14. 如图，Rt△ABC中，∠C＝90°，AD为△ABC的角平分线，与BC相交于点D，若CD＝4，AB＝15，则△ABD的面积是．

查看试题解析
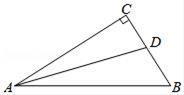15. 如图，在△ABC中，AB＝AC ，点D在AC上，过点D作DF⊥BC于点F ，且BD＝BC＝AD ，则∠CDF的度数为．

查看试题解析
16. 如图，△ABC角平分线AE、CF交于点P ， BD是△ABC的高，点H在AC上，AF＝AH ，下列结论：①∠APC＝90°+ $\frac{1}{2} ∠$ ABC；②PH平分∠APC；③若BC＞AB ，连接BP ，则∠DBP＝∠BAC﹣∠BCA；④若PH∥BD ，则△ABC为等腰三角形，其中正确的结论有（填序号）．

查看试题解析

三、解答题

17. 计算

(1)、（2﹣ $\sqrt{3}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣²

(2)、（﹣3a²）³÷6a+ $\frac{3}{2}$ a²•a³

查看试题解析
18. 计算

(1)、（x+1）²﹣（x+1）（x﹣1）

(2)、 $\frac{(x + 2) (2 x + 1)}{2 x}$ ﹣x﹣2

查看试题解析
19. 如图， $D$ 、 $C$ 、 $F$ 、 $B$ 四点在一条直线上， $A B = D E$ ， $A C ⊥ B D$ ， $E F ⊥ B D$ ，垂足分别为点 $C$ 、点 $F$ ， $C D = B F$ ．

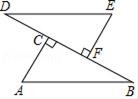
求证：

(1)、 $Δ A B C ≅ Δ E D F$ ；

(2)、 $A B / / D E$ ．

查看试题解析
20. 如图，已知A（﹣2，4），B（4，2），C（2，﹣1）

(1)、作△ABC关于x轴的对称图形△A₁B₁C₁ ，写出点C关于x轴的对称点C₁的坐标；

(2)、P为x轴上一点，请在图中找出使△PAB的周长最小时的点P并直接写出此时点P的坐标（保留作图痕迹）．

查看试题解析
21. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要时间与原计划生产450台机器所需时间相同．

(1)、现在平均每天生产多少台机器；

(2)、生产3000台机器，现在比原计划提前几天完成．

查看试题解析
22. 化简：（ $\frac{2 x^{2} + 2 x}{x^{2} - 1}$ ﹣ $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ ） ÷ $\frac{x}{x + 1}$ ，并解答：

(1)、当x=3时，求原式的值；

(2)、原式的值能等于﹣1吗？为什么？

查看试题解析
23. 如图，已知△ABC中AB＝AC ，在AC上有一点D ，连接BD ，并延长至点E ，使AE＝AB ．

(1)、画图：作∠EAC的平分线AF ， AF交DE于点F（用尺规作图，保留作图痕迹，不写作法）；

(2)、在（1）的条件下，连接CF ，求证：∠ABE＝∠ACF；

(3)、若AC＝8，∠E＝15°，求三角形ABE的面积．

查看试题解析
24. 因式分解是把多项式变形为几个整式乘积的形式的过程．

(1)、设有多项式x²+2x﹣m分解后有一个因式是x+4，求m的值．

(2)、若有甲、乙两个等容积的长方体容器，甲容器长为x﹣1，宽为x﹣2．体积为x⁴﹣x³+ax²+bx﹣6，（x为整数），乙容器的底面是正方形．
①求出a ， b的值；

②分别求出甲、乙两容器的高．（用含x的代数式表示）

查看试题解析
25. 在Rt△ABC中，∠B＝90°，AB＝8，CB＝5，动点M从C点开始沿CB运动，动点N从B点开始沿BA运动，同时出发，两点均以1个单位/秒的速度匀速运动（当M运动到B点即同时停止），运动时间为t秒．

(1)、AN＝；CM＝．（用含t的代数式表示）

(2)、连接CN ， AM交于点P ．
①当t为何值时，△CPM和△APN的面积相等？请说明理由．

②当t＝3时，试求∠APN的度数．

查看试题解析