广东省佛山市禅城区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 下列实数中的无理数是( )A、0.7 B、
 C、π
D、-8
2. 估计 +1的值( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间3. 直线 不经过的象限是A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 数据3,6,7,4,x的平均数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、65. 方程2x﹣ =0,3x+y=0,2x+xy=1,3x+y﹣2x=0,x2﹣x+1=0中,二元一次方程的个数是( )A、5个 B、4个 C、3个 D、2个6. 直角三角形的斜边为10cm,两直角边之比为3:4,那么这个直角三角形的周长为( )A、17cm B、15cm C、20cm D、24cm7. 如图,∠1=65°,CD∥EB,则∠B的度数为( )
C、π
D、-8
2. 估计 +1的值( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间3. 直线 不经过的象限是A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 数据3,6,7,4,x的平均数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、65. 方程2x﹣ =0,3x+y=0,2x+xy=1,3x+y﹣2x=0,x2﹣x+1=0中,二元一次方程的个数是( )A、5个 B、4个 C、3个 D、2个6. 直角三角形的斜边为10cm,两直角边之比为3:4,那么这个直角三角形的周长为( )A、17cm B、15cm C、20cm D、24cm7. 如图,∠1=65°,CD∥EB,则∠B的度数为( ) A、115° B、110° C、105° D、65°8. 已知点 , , 都在直线 上,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图是由线段AB,CD,DF,BF,CA组成的平面图形, ,则 的度数为( )
A、115° B、110° C、105° D、65°8. 已知点 , , 都在直线 上,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图是由线段AB,CD,DF,BF,CA组成的平面图形, ,则 的度数为( ) A、 B、 C、 D、10. 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家 妈妈8:30从家出发,乘车沿相同路线去姥姥家 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是( )
A、 B、 C、 D、10. 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家 妈妈8:30从家出发,乘车沿相同路线去姥姥家 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是( ) A、9:00妈妈追上小亮 B、妈妈比小亮提前到达姥姥家 C、小亮骑自行车的平均速度是 D、妈妈在距家13km处追上小亮
A、9:00妈妈追上小亮 B、妈妈比小亮提前到达姥姥家 C、小亮骑自行车的平均速度是 D、妈妈在距家13km处追上小亮二、填空题
-
11. 点 到x轴的距离为 .12. 如图,每个小方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么用表示C点的位置.
 13. 如图,在 中, ,D点是 和 角平分线的交点,则 .
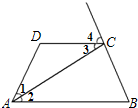
13. 如图,在 中, ,D点是 和 角平分线的交点,则 . 14. 禅城区某一中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量 , , , , ,若每种植1平方米草皮需要300元,总共需投入元
14. 禅城区某一中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量 , , , , ,若每种植1平方米草皮需要300元,总共需投入元
三、解答题
-
15. 计算:16. .17. 如图,已知 , ,求证:AC平分 .
 18. 如图,一次函数的图象分别与x轴、y轴交于点 , .
18. 如图,一次函数的图象分别与x轴、y轴交于点 , . (1)、求函数的表达式.(2)、在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.19. 目前节能灯在城市已基本普及,今年某省面向农村地区推广,为响应号召,某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
(1)、求函数的表达式.(2)、在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.19. 目前节能灯在城市已基本普及,今年某省面向农村地区推广,为响应号召,某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:进价 元 只
售价 元 只
甲种节能灯
30
40
乙种节能灯
35
50
(1)、求甲、乙两种节能灯各进多少只?(2)、全部售完100只节能灯后,该商场获利多少元?20.叙述并证明“三角形的内角和定理”.(要求根据下图写出已知、求证并证明)
 21. 某校要从甲、乙两个跳远运动员中选一人参加一项比赛,在最近的10次选拨赛中,他们的成绩 单位: 如下:
21. 某校要从甲、乙两个跳远运动员中选一人参加一项比赛,在最近的10次选拨赛中,他们的成绩 单位: 如下:甲:585,596,610,598,612,597,604,600,613,601
乙:613,618,580,574,618,593,585,590,598,624
(1)、分别求甲、乙的平均成绩;(2)、分别求甲、乙这十次成绩的方差;(3)、这两名运动员的运动成绩各有什么特点?历届比赛成绩表明,成绩达到 就很可能夺冠你认为应选谁参加比赛?22. 在 中,AB,BC,AC三边的长分别为 、 、 ,求这个三角形的面积 小辉同学在解答这道题时,先建立一个正方形网格 每个小正方形的边长为 ,再在网格中画出格点 的三个顶点都在正方形的顶点处 ,如图所示,这样不需要求 的高,而借用网格就能计算出它的面积. (1)、请你将 的面积直接填写在横线上.(2)、已知 ,DE、EF、DF三边的长分别为 、 、 ,
(1)、请你将 的面积直接填写在横线上.(2)、已知 ,DE、EF、DF三边的长分别为 、 、 ,① 是否为直角形,并说明理由.
②求这个三角形的面积.
23. 如图1,BC⊥AF于点C , ∠A+∠1=90°.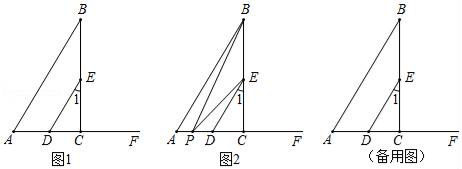 (1)、求证:AB∥DE;(2)、如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB , PE . 则∠ABP , ∠DEP , ∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A , D , C重合的情况)?并说明理由.
(1)、求证:AB∥DE;(2)、如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB , PE . 则∠ABP , ∠DEP , ∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A , D , C重合的情况)?并说明理由.