辽宁省沈阳市铁西区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的几何体的主视图是（　　）

A、 B、 C、 D、

查看试题解析
2. 方程（a﹣2）x²+ax+b＝0是关于x的一元二次方程，则a的取值范围是（　　）

A、a≠0 B、a≠2 C、a＝2 D、a＝0

查看试题解析
3. 如图，在矩形ABCD中，对角线AC、BD相交于点O，且∠AOD＝120°，AC＝6，则图中长度为3的线段有（）

A、2条 B、4条 C、5条 D、6条

查看试题解析
4. 九年级一班在参加学校4×100米接力赛时，安排了甲，乙，丙，丁四位选手，他们比赛的顺序由抽签随机决定，则丙跑第一棒的概率为（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{8}$ C、 $\frac{1}{12}$ D、 $\frac{1}{16}$

查看试题解析
5. 已知反比例函数y＝ $\frac{6}{x}$ ，当1＜x＜3时，y的取值范围是（）

A、0＜y＜1 B、1＜y＜2 C、2＜y＜6 D、y＞6

查看试题解析
6. 抛物线y＝3x²﹣6x+4的顶点坐标是（　　）

A、（1，1） B、（﹣1，1） C、（﹣1，﹣2） D、（1，2）

查看试题解析
7. 已知 $\frac{b}{a} = \frac{5}{13}$ ，则 $\frac{a - b}{a + b}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{9}{4}$ D、 $\frac{4}{9}$

查看试题解析
8. 一元二次方程x²﹣2x＝0的两根分别为x₁和x₂ ，其中x₁＜x₂ ，则x₁²﹣2x₂²的值为（　　）

A、﹣4 B、﹣8 C、8 D、4

查看试题解析
9. 如图，▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）

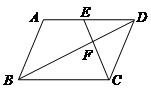A、3：2 B、3：1 C、1：1 D、1：2

查看试题解析
10. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（　　）

A、选①② B、选①③ C、选②④ D、选②③

查看试题解析

二、填空题

11. 已知反比例函数y= $\frac{k - 1}{x}$ （k是常数，k≠1）的图象有一支在第二象限，那么k的取值范围是．

查看试题解析
12. 边长为3cm的菱形的周长是.

查看试题解析
13. 一元二次方程（x+1）（x﹣3）＝2x﹣5实数根.（填“有”或“没有”）

查看试题解析
14. 已知直线y＝k₁x（k₁≠0）与反比例函数y＝ $\frac{k_{2}}{x}$ （k₂≠0）的图象交于M.N两点，若点M的坐标是（1，2），则点N的坐标是.

查看试题解析
15. 一根1.5米长的标杆直立在水平地面上，它在阳光下的影长为2.1米，此时标杆旁边一棵杨树的影长为10.5米，则这棵杨树高为米.

查看试题解析
16. 如图，抛物线C₁：y＝x²﹣2x﹣3与x轴交于A、B两点，点A在点B的左侧，将抛物线C₁向上平移1个单位得到抛物线C₂ ，点Q（m，n）在抛物线C₂上，其中m＞0且n＜0，过点P作PQ∥y轴交抛物线C₁于点P，点M是x轴上一点，当以点P、Q、M为顶点的三角形与△AOQ全等时，点M的横坐标为.

查看试题解析

三、解答题

17. 解方程：2x²+x＝4x﹣1

查看试题解析
18. 如图，一次函数 $y = m x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A (3 ， 1)$ ， $B (- \frac{1}{2}$ ， $n)$ 两点．

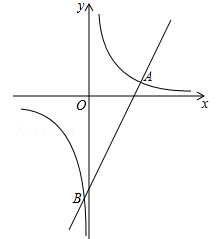(1)、求该反比例函数的解析式；

(2)、求 $n$ 的值及该一次函数的解析式．

查看试题解析
19. 在一个不透明的布袋里共装有3个球（除颜色不同外其余都相同），其中2个是红球，1个是白球，从中任意摸出一个球，记下颜色后放回，搅匀，再任意摸出一个球，请用树状图或列表法求两次摸出的都是白球的概率.

查看试题解析
20. 小王经营的网店专门销售某种品牌的一种保温杯，成本为30元/只，每天销售量y（只）与销售单价x（元）之间的关系式为y＝﹣10x+700（40≤x≤55），求当销售单价为多少元时，每天获得的利润最大？最大利润是多少元？

查看试题解析
21. 如图，四边形ABGH、BCFG、CDEF是边长为1的正方形，连接BH、CH、DH，求证：∠ABH+∠ACH+∠ADH＝90°.

查看试题解析
22. 已知关于x的一元二次方程（x﹣1）（x﹣4）＝a² ，其中a为常数.

(1)、求证：此方程有两个不相等的实数根；

(2)、当|a﹣2|＝0时，求此方程的根.

查看试题解析
23. 如图，在平面直角坐标系中，点A的坐标为（5，0），点B的坐标为（8，4），点C的坐标为（3，4），连接AB、BC、OC

(1)、求证四边形OABC是菱形；

(2)、直线l过点C且与y轴平行，将直线l沿x轴正方向平移，平移后的直线交x轴于点P.
①当OP：PA＝3：2时，求点P的坐标；

②点Q在直线1上，在直线l平移过程中，当△COQ是等腰直角三角形时，请直接写出点Q的坐标.

查看试题解析
24. Rt△ABC中，∠ACB＝90°，AC＝3，BC＝7，点P是边AC上不与点A、C重合的一点，作PD∥BC交AB边于点D.

(1)、如图1，将△APD沿直线AB翻折，得到△AP'D，作AE∥PD.求证：AE＝ED；

(2)、将△APD绕点A顺时针旋转，得到△AP'D'，点P、D的对应点分别为点P'、D'，
①如图2，当点D'在△ABC内部时，连接P′C和D'B，求证：△AP'C∽△AD'B；

②如果AP：PC＝5：1，连接DD'，且DD'＝ $\sqrt{2}$ AD，那么请直接写出点D'到直线BC的距离.

查看试题解析
25. 如图，抛物线y＝ $\frac{8}{15}$ x²+bx+c过点A（2，0）和B（3，3）.

(1)、求抛物线的表达式；

(2)、点M在第二象限的抛物线上，且∠MBO＝∠ABO.
①直线BM交x轴于点N，求线段ON的长；
②延长BO交抛物线于点C，点P是平面内一点，连接PC、OP，当△POC∽△MOB时，请直接写出点P的坐标.

查看试题解析