湖北省丹江口市2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-12-30 类型：期末考试
一、单选题
-
1. 下面所列图形中是中心对称图形的为（ ）A、
B、
C、
D、
2. 不透明袋子中有2个红球、3个绿球，这些球除颜色外其它无差别．从袋子中随机取出1个球，则（ ）A、能够事先确定取出球的颜色 B、取到红球的可能性更大 C、取到红球和取到绿球的可能性一样大 D、取到绿球的可能性更大3. 已知关于x的函数y＝(m﹣1)xm是反比例函数，则其图象（ ）A、位于一、三象限 B、位于二、四象限 C、经过一、三象限 D、经过二、四象限4. 已知点A(a，1)与点B(5，b)关于原点对称，则a、b值分别是（ ）A、a=5，b=1 B、a=﹣5，b=1 C、a=﹣5，b=﹣1 D、a=1，b=55. 抛物线y=﹣ x2向左平移1个单位长度得到抛物线的解析式为（ ）A、y=﹣ （x+1）2 B、y=﹣ （x﹣1）2 C、y=﹣ x2+1 D、y=﹣ x2﹣16. 如图，AB是⊙O的直径，点C，D在⊙O上.若∠ABD＝50°，则∠BCD的度数为（ ）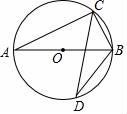
A、30° B、35° C、40° D、45°7. 如图，光源P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB＝2m，CD＝6m，点P到CD的距离是2.7m，则AB离地面的距离为（ ）m.
A、2.1 B、2 C、1.8 D、1.68. 如图，在△ABC中，AC＝6，BC＝8，AB＝10，D，E分别是AC，BC的中点，则以DE为直径的圆与AB的位置关系是（ ）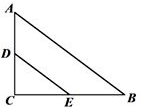
A、相切 B、相交 C、相离 D、无法确定9. 若m、n(m＜n)是关于x的一元二次方程3﹣(x﹣a)(x﹣b)＝0的两个根，且a＜b，则m，n，b，a的大小关系是（ ）A、m＜a＜b＜n B、a＜m＜n＜b C、b＜n＜m＜a D、n＜b＜a＜m10. 如图，直线y= x与双曲线y= （x＞0）交于点A，将直线y= x向右平移3个单位后，与双曲线y= （x＞0）交于点B，与x轴交于点C，若 =2，则k=（ ）
A、 B、4 C、6 D、二、填空题
-
11. 如图为测量平地上一块不规则区域(图中的阴影部分)的面积，画一个边长为5m的正方形，使不规则区域落在正方形内，现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的)，经过大量重复投掷试验，发现小石子落在不规则区域的频率稳定在常数0.2附近，由此可估计不规则区域的面积是m2.
12. 在一幢高125m的大楼上掉下一个苹果，苹果离地面的高度h(m)与时间t(s)大致有如下关系：h＝125﹣5t2.秒钟后苹果落到地面.13. 如图，在平面直角坐标系中，三角形②是由三角形①绕点P旋转后所得的图形，则旋转中心P的坐标是.
14. 如图，A是反比例函数 的图象上一点，过点A作AB∥y轴交反比例函数 的图象交于点B，已知△OAB的面积为5，则k的值为.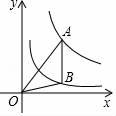
15. 如图，圆锥形的烟囱冒的底面直径是80cm，母线长是50cm，制作一个这样的烟囱冒至少需要cm2的铁皮.
16. 如图，正方形ABCD中，AB＝3cm，以B为圆心，1cm长为半径画⊙B，点P在⊙B上移动，连接AP，并将AP绕点A逆时针旋转90°至AP′，连接BP′.在点P移动的过程中，BP′长度的最小值为cm.
三、解答题
-
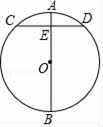
17. 已知y与x﹣1成反比例，且当x＝2时，y＝3，求当y＝6时x的值.18. 在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现代语言表述为：如图，AB为⊙O的直径，弦CD⊥AB于点E，AE＝1寸，CD＝10寸，求直径AB的长.请你解答这个问题.
19. 不透明的袋子中装有4个相同的小球，它们除颜色外无其它差别，把它们分别标号：1、2、3、4.(1)、随机摸出一个小球后，放回并摇匀，再随机摸出一个，用列表或画树状图的方法求出“两次取的球标号相同”的概率；(2)、随机摸出两个小球，直接写出“两次取出的球标号和为奇数”的概率.20. 如图，一次函数y1＝﹣x+2的图象与反比例函数y＝ 的图象交于点A(﹣1，m)，点B(n，﹣1).
(1)、求反比例函数的解析式；(2)、当y1＞y时，直接写出x的取值范围；(3)、求△AOB的面积.21. 已知二次函数y＝x2﹣2x+k﹣1的图象与x轴交于不同的两点A(x1 ， 0)，B(x2 ， 0).(1)、求k的取值范围；(2)、若AB＝2，求k的值.22. 小明妈妈开网店销售某品牌童装，每件售价110元，每月可卖200件，为了促销，该网店决定降价销售.市场调查反映：每降价1元，每月可多卖20件.已知该品牌童装每件成本价80元，设该品牌童装每件售价x元，每月的销售量为y件.(1)、求y与x之间的函数关系式；(2)、当每件售价定为多少元时，每月的销售利润最大，最大利润多少元？23. 如图，AB为⊙O的直径，C、F为⊙O上两点，且点C为弧BF的中点，过点C作AF的垂线，交AF的延长线于点E，交AB的延长线于点D.
(1)、求证：DE是⊙O的切线；(2)、若AE＝3，DE＝4，求⊙O的半径的长.24. 以△ABC的边AB，AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，M为EG的中点，连接AM.
(1)、如图1，∠BAC=90°，试判断AM与BC关系？(2)、如图2，∠BAC≠90°，图1中的结论是否成立？若不成立，说明理由；若成立，给出证明.25. 如图，二次函数y= x2+bx+c的图象交x轴于A，D两点，并经过B点，对称轴交x轴于点C，连接BD，BC，已知A点坐标是（2，0），B点的坐标是（8，6）
(1)、求二次函数的解析式.(2)、求该函数图象的顶点坐标及D点的坐标.(3)、抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S△ADP= S△BCD？若存在，直接写出所有符合条件的点P的坐标；若不存在.请说明理由.