2011年广西河池市中考数学试卷

试卷更新日期：2017-07-31 类型：中考真卷

进入出卷网下载

一、选择题

1. 有理数﹣3的相反数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 函数y= $\sqrt{x - 1}$ 的自变量x的取值范围是（）

A、x＞1 B、x＜1 C、x≥1 D、x≤1

查看试题解析
3. 如图，AB∥CD，AC与BD相交于点O，∠A=30°，∠COD=105°．则∠D的大小是（）

A、30° B、45° C、65° D、75°

查看试题解析
4. 下列运算中，正确的是（）

A、x⁶÷x²=x³ B、（﹣3x）²=6x² C、3x²﹣2x²=x D、x³•x=x⁴

查看试题解析
5. 解集在数轴上表示为如图所示的不等式组是（）

A、 ${\begin{cases} x > - 1 \\ x \geq 2 \end{cases}$ B、 ${\begin{cases} x < - 1 \\ x \leq 2 \end{cases}$ C、 ${\begin{cases} x < - 1 \\ x \geq 2 \end{cases}$ D、 ${\begin{cases} x > - 1 \\ x \leq 2 \end{cases}$

查看试题解析
6. 五箱苹果的质量分别为（单位：千克）：18，20，21，22，19．则这五箱苹果质量的平均数和中位数分别为（）

A、19和20 B、20和19 C、20和20 D、20和21

查看试题解析
7. 把二次函数y=x²的图象沿着x轴向右平移2个单位，再向上平移3个单位，所得到的函数图象的解析式为（）

A、y=（x+2）²+3 B、y=（x﹣2）²+3 C、y=（x+2）²﹣3 D、y=（x﹣2）²﹣3

查看试题解析
8. 如图是一个几何体的三视图，则此几何体是（）

A、圆柱 B、棱柱 C、圆锥 D、棱台

查看试题解析
9. 如图，A（1，0）、B（7，0），⊙A、⊙B的半径分别为1和2，将⊙A沿x轴向右平移3个单位，则此时该圆与⊙B的位置关系是（）

A、外切 B、相交 C、内含 D、外离

查看试题解析
10. 如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC的度数是（）

A、35° B、55° C、65° D、70°

查看试题解析
11. 如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，下述结论错误的是（）

A、BD平分∠ABC B、△BCD的周长等于AB+BC C、AD=BD=BC D、点D是线段AC的中点

查看试题解析
12. 如图，在平行四边形ABCD中，E为AB的中点，F为AD上一点，EF交AC于G，AF=2cm，DF=4cm，AG=3cm，则AC的长为（）

A、9cm B、14cm C、15cm D、18cm

查看试题解析

二、填空题

13. 分解因式：x²﹣9= ．

查看试题解析
14. 计算： $\sqrt[3]{27} - \frac{\sqrt{2} \times \sqrt{6}}{\sqrt{3}}$ = ．

查看试题解析
15. 某校为了了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐次数在20～25次之间的频数是．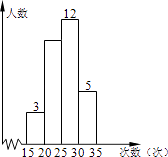

查看试题解析
16. 如图是二次函数y₁=ax²+bx+c（a≠0）和一次函数y₂=mx+n（m≠0）的图象，当y₂＞y₁ ， x的取值范围是．

查看试题解析
17. 如图所示：用一个半径为60cm，圆心角为150°的扇形围成一个圆锥，则这个圆锥的底面半径为cm．

查看试题解析
18. 如图，在Rt△ABC中，∠ABC是直角，AB=3，BC=4，P是BC边上的动点，设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是．

查看试题解析

三、解答题.

19. 计算：2011⁰+（ $\frac{1}{2}$ ）^﹣¹+4sin45°﹣|﹣ $\sqrt{8}$ |

查看试题解析
20. 先化简，再求值：（x+3）²﹣（x﹣1）（x﹣2），其中x=﹣1．

查看试题解析
21. 如图，在平行四边形ABCD中，点E、F分别是AD、BC的中点，AC与EF相交于点O．

(1)、过点B作AC的平行线BG，延长EF交BG于H；

(2)、在（1）的图中，找出一个与△BHF全等的三角形，并证明你的结论．

查看试题解析
22. 某班毕业晚会设计了即兴表演节目的摸球游戏，在一个不透明的盒子里装有4个分别标有数字1、2、3、4的乒乓球，这些球除数字外，其它完全相同．晚会上每位同学必须且只能做一次摸球游戏．游戏规则是：从盒子里随机摸出一个球，放回搅匀后，再摸出一个球，若第二次摸出的球上的数字小于第一次摸出的球上的数字，就要给大家即兴表演一个节目．

(1)、参加晚会的同学性别比例如图，女生有18人，则参加晚会的学生共有多少人；

(2)、用列表法或树形图法求出晚会的某位同学即兴表演节目的概率；

(3)、估计本次晚会上有多少名同学即兴表演节目？

查看试题解析
23. 大众服装店今年4月用4000元购进了一款衬衣若干件，上市后很快售完，服装店于5月初又购进同样数量的该款衬衣，由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元，结果第二批衬衣进货用了5000元．

(1)、第一批衬衣进货时的价格是多少？

(2)、第一批衬衣售价为120元/件，为保证第二批衬衣的利润率不低于第一批衬衣的利润率，那么第二批衬衣每件售价至少是多少元？
（提示：利润=售价﹣成本，利润率= $\frac{利润}{成本} \times 100%$ ）

查看试题解析
24. 如图，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边的活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡，改变活动托盘B与点O的距离x（cm），观察活动托盘B中砝码的质量y（g）的变化情况．实验数据记录如下表：
x（cm）
10
15
20
25
30
y（g）
30
20
15
12
10

(1)、把上表中（x，y）的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点；

(2)、观察所画的图象，猜测y与x之间的函数关系，求出函数关系式并加以验证；

(3)、当砝码的质量为24g时，活动托盘B与点O的距离是多少cm？

(4)、当活动托盘B往左移动时，应往活动托盘B中添加还是减少砝码？

查看试题解析
25. 如图1，在△ABO中，∠OAB=90°，∠AOB=30°，OB=8．以OB为一边，在△OAB外作等边三角形OBC，D是OB的中点，连接AD并延长交OC于E．

(1)、求点B的坐标；

(2)、求证：四边形ABCE是平行四边形；

(3)、如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．

查看试题解析
26.
已知直线l经过A（6，0）和B（0，12）两点，且与直线y=x交于点C．

(1)、求直线l的解析式；

(2)、
若点P（x，0）在线段OA上运动，过点P作l的平行线交直线y=x于D，求△PCD的面积S与x的函数关系式；S有最大值吗？若有，求出当S最大时x的值；

(3)、若点P（x，0）在x轴上运动，是否存在点P，使得△PCA成为等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

查看试题解析

x（cm）	10	15	20	25	30
y（g）	30	20	15	12	10