广东省普宁市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

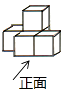
1. 在﹣4，2，﹣1，3这四个数中，比﹣2小的数是（）

A、﹣4 B、2 C、﹣1 D、3

查看试题解析
2. 下图是由五个相同的小正方体搭成的一个几何体，从左面看到的几何体的形状图是（）.

A、 B、 C、 D、

查看试题解析
3. 下列语句正确的是 $($ $)$

A、 $- \frac{2 vt}{3}$ 的系数是 $- 2$ B、0是代数式 C、手电筒发射出去的光可看作是一条直线 D、正方体不是棱柱

查看试题解析
4. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为4400000000人，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、4.4×10¹⁰

查看试题解析
5. 下列计算正确的是 $($ $)$

A、 $(- 14) - (+ 5) = 9$ B、 $0 - (- 3) = 0 + (- 3)$ C、 $(- 3) \times (- 3) = - 6$ D、 $| 3 - 5 | = 2$

查看试题解析
6. 如图所示，用经过A、B、C三点的平面截去正方体的一角，变成一个新的多面体，这个多面体的面数是 $($ $)$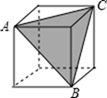

A、8 B、7 C、6 D、5

查看试题解析
7. 如图，甲从A点出发向北偏东70°方向走至点B，乙从A点出发向南偏西15°方向走至C，则∠BAC的度数是（）

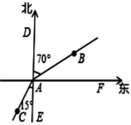A、85° B、160° C、105° D、125°

查看试题解析
8. 下列调查中，适合用普查（全面调查）方式的是（）

A、了解一批袋装食品是否含有防腐剂 B、了解某班学生“50米跑”的成绩 C、了解江苏卫视“非诚勿扰”节目的收视率 D、了解一批灯泡的使用寿命

查看试题解析
9. 有理数a、b在数轴上的位置如图所示，则化简|a﹣b|+a的结果为（）

A、b B、﹣b C、﹣2a﹣b D、2a﹣b

查看试题解析
10. 某工程，甲独做需12天完成，乙独做需8天完成，现由甲先做3天，乙再参加合做，求完成这项工程共用的时间．若设完成此项工程共用x天，则下列方程正确的是（）

A、 $\frac{x + 3}{12}$ + $\frac{x}{8}$ =1 B、 $\frac{x + 3}{12}$ + $\frac{x - 3}{8}$ =1 C、 $\frac{x}{12}$ + $\frac{x}{8}$ =1 D、 $\frac{x}{12}$ + $\frac{x - 3}{8}$ =1

查看试题解析

二、填空题

11. 若3a³b⁵ⁿ^﹣2与10b^3m+na^m^﹣1是同类项，则m= ， n= ．

查看试题解析
12. 已知x=2是关于x的一元一次方程1-2ax=x+a的解，则a的值为．

查看试题解析
13. 如图，点C在线段AB上，点D是AC的中点，如果 $BC = 1.5 CD$ ， $AB = 10.5$ 厘米，那么BC的长为厘米．

查看试题解析
14. 甲、乙两人参加某体育项目训练，为了便于研究，把最近五次的训练成绩绘制成如图所示的折线统计图，则的训练成绩比较好 $. ($ 选填甲或乙 $)$ ．

查看试题解析
15. 如图，某长方体的底面是长为4cm，宽为2cm的长方形，如果从左面看这个长方体时看到的图形面积为6cm² ，则这个长方体的体积等于．

查看试题解析
16. 已知整数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4} \dots$ 满足下列条件： $a_{1} = 0$ ， $a_{2} = - | a_{1} + 1 |$ ， $a_{3} = - | a_{2} + 2 |$ ， $a_{4} = - | a_{3} + 3 |$ ， $\dots$ ，依此类推，则 $a_{2019}$ 的值为．

查看试题解析

三、解答题

17. 计算： ${(- 3)}^{2} - 1 \frac{1}{2} \times \frac{2}{9} - 6 \div | - \frac{2}{3} |^{2} - (- 2^{2}) .$

查看试题解析
18. 计算： ${(- 1)}^{2019} \div {[(- 4) \times (- \frac{5}{8}) \div (- \frac{1}{3}) + (- 3) \times (+ \frac{1}{2})] \times {(- 2)}^{2} + (- 6)}$

查看试题解析
19. 解方程： $x - \frac{x - 2}{5} = \frac{2 x - 5}{3} - 3$ ．

查看试题解析
20. 某商场计划购进甲，乙两种节能灯共1200个，这两种节能灯的进价、售价如下表：

进价 $($ 元 $/$ 个 $)$

售价 $($ 元 $/$ 个 $)$

甲型

25

30

乙型

45

60

(1)、若商场预计进货款为44000元，则这两种节能灯应各购买多少个？

(2)、如何进货，使销售完节能灯时，商场获得的利润恰好是成本的 $30 %$ ，此时利润为多少元？

查看试题解析
21. 先化简，再求值 $- (2 x^{2} - y^{2}) + 3 (2 y^{2} - 3 x^{2}) - 2 (y^{2} - 2 x^{2})$ ，其中 $x = - 1$ ， $y = 2$ ．

查看试题解析
22. 作图题：如图，已知点A，点B，直线l及l上一点M.

(1)、连接MA，并在直线l上作出一点N，使得点N在点M的左边，且满足MN＝MA；

(2)、请在直线l上确定一点O，使点O到点A与点O到点B的距离之和最短，并写出画图的依据.

查看试题解析
23. 随着互联网的发展，同学们的学习习惯也有了改变，一些同学在做题遇到困难时，喜欢上网查找答案．针对这个问题，某校调查了部分学生对这种做法的意见(分为：赞成、无所谓、反对)，并将调查结果绘制成图1和图2两个不完整的统计图．
请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了多少名学生?

(2)、将图1补充完整；

(3)、求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数；

(4)、根据抽样调查结果，请你估计该校1500名学生中有多少名学生持“无所谓”意见．

查看试题解析
24. 已知，O是直线AB上的一点，∠COD是直角，OE平分∠BOC．

(1)、如图1.
①若∠AOC＝60°，求∠DOE的度数；

②若∠AOC＝α，直接写出∠DOE的度数(用含α的式子表示)；

(2)、将图1中的∠DOC绕点O顺时针旋转至图2的位置，试探究∠DOE和∠AOC的度数之间的关系，写出你的结论，并说明理由．

查看试题解析
25. 如图1，P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动，在直角三角形ABC中，∠A＝90°，若AB＝16厘米，AC＝12厘米，BC＝20厘米，如果P、Q同时出发，用t（秒）表示移动时间，那么：

(1)、如图1，若P在线段AB上运动，Q在线段CA上运动，试求出t为何值时，QA＝AP

(2)、如图2，点Q在CA上运动，试求出t为何值时，三角形QAB的面积等于三角形ABC面积的 $\frac{1}{4}$ ；

(3)、如图3，当P点到达C点时，P、Q两点都停止运动，试求当t为何值时，线段AQ的长度等于线段BP的长的 $\frac{1}{4}$

查看试题解析

	进价 $($ 元 $/$ 个 $)$	售价 $($ 元 $/$ 个 $)$
甲型	25	30
乙型	45	60