湖北省大冶市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 若反比例函数y=﹣ 的图象经过点A(2,m),则m的值是( )A、 B、2 C、﹣ D、﹣22. 亚洲陆地面积约为4400万平方千米,将44000000科学记数法表示为( )A、4.4×107 B、4.4×106 C、0.44×107 D、4.4×1033. 2015年某县 总量为1000亿元,计划到2017年全县 总量实现1210亿元的目标,如果每年的平均增长率相同,那么该县这两年 总量的年平均增长率为( )A、 B、 C、 D、4. 在一个有10万人的小镇,随机调查了1000人,其中有120人周六早上观看中央电视台的“朝闻天下”节目,那么在该镇随便问一个人,他在周六早上观看中央电视台的“朝闻天下”节目的概率大约是( )A、 B、 C、 D、5. 如图,在⊙O中,弦AB、CD相交于点M,连接BC、AD,∠AMD=100°,∠A=30°,则∠B=( )
 A、40° B、45° C、50° D、60°6. 如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
A、40° B、45° C、50° D、60°6. 如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( ) A、2 cm B、4 cm C、6 cm D、8 cm7. 如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )
A、2 cm B、4 cm C、6 cm D、8 cm7. 如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( ) A、ac<0 B、2a+b=0 C、对于任意x均有ax2+bx≥a+b D、4a+2b+c>08.
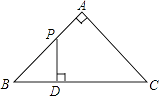
A、ac<0 B、2a+b=0 C、对于任意x均有ax2+bx≥a+b D、4a+2b+c>08.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
 A、
A、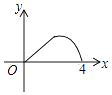 B、
B、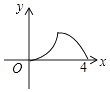 C、
C、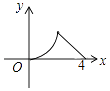 D、
D、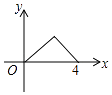
二、填空题
-
9. 二次函数y=4(x﹣3)2+7的图象的顶点坐标是 .10. 如图,转盘中6个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,指针指向奇数的概率是.
 11. 已知关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根x1、x2.若x1﹣2x2=6,则实数m的值为.12. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是.
11. 已知关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根x1、x2.若x1﹣2x2=6,则实数m的值为.12. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是. 13. 如图,已知Rt△ABC中,∠ACB=90° AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
13. 如图,已知Rt△ABC中,∠ACB=90° AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= . 14. 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y= (x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2018=.
14. 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y= (x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2018=.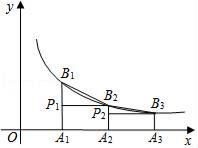
三、解答题
-
15. 计算:﹣22+(π﹣2019)0+( )﹣1+|1﹣ |16. 先化简,再求值:(2﹣ )÷ ,其中x= ﹣3.17. 解不等式组 ,把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
 18. 如图,已知一次函数 与反比例函数 的图象交于 , 两点.
18. 如图,已知一次函数 与反比例函数 的图象交于 , 两点.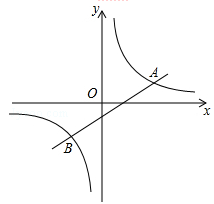 (1)、求一次函数与反比例函数的解析式;(2)、请根据图象直接写出 时 的取值范围.19. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)、求一次函数与反比例函数的解析式;(2)、请根据图象直接写出 时 的取值范围.19. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB. (1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为 ,OP=1,求BC的长.20. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有 1个,若从中随机摸出一个球,这个球是白球的概率为(1)、求袋子中白球的个数;(请通过列式或列方程解答);
(1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为 ,OP=1,求BC的长.20. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有 1个,若从中随机摸出一个球,这个球是白球的概率为(1)、求袋子中白球的个数;(请通过列式或列方程解答);
(2)、随机摸出一个球后,不放回,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)21. 某文具店从市场得知如下信息:A品牌计算器
B品牌计算器
进价(元/台)
70
100
售价(元/台)
90
140
该文具店计划一次性购进这两种品牌计算器共50台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)、求y与x之间的函数关系式;(2)、若全部销售完后,获得的利润为1200元,则购进A、B两种品牌计算器的数量各是多少台?(3)、若购进计算器的资金不超过4100元,求该文具店可获得的最大利润是多少元?22. (1)、探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
(1)、探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系时,仍有EF=BE+DF;
(2)、拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2 ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.23. 如图,一次函数 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点. (1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
(1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.