河南省洛阳市汝阳县2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 若 无意义,则x的取值范围是( )A、x>0 B、x≤3 C、x>3 D、x≥32. 已知x=2是一元二次方程x2+mx+2=0的一个根,则m=( )A、-3 B、3 C、0 D、0或33. 已知α是锐角,sinα=cos60°,则α等于( )A、30° B、45° C、60° D、不能确定4.
如图,已知直线a∥b∥c , 直线m、n与直线a、b、c分别交于点A、C、E、B、D、F , AC=4,CE=6,BD=3,则BF=( ).
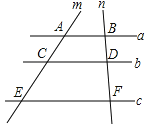 A、7 B、7.5 C、8 D、8.55. 某存折的密码是一个六位数字(每位可以是0),由于小王忘记了密码的首位数字,则他能一次说对密码的概率是( )A、 B、 C、 D、6. 在同一直角坐标系中,函数y=ax2+b与y=ax+b(a,b都不为0)的图象的相对位置可以是( )A、
A、7 B、7.5 C、8 D、8.55. 某存折的密码是一个六位数字(每位可以是0),由于小王忘记了密码的首位数字,则他能一次说对密码的概率是( )A、 B、 C、 D、6. 在同一直角坐标系中,函数y=ax2+b与y=ax+b(a,b都不为0)的图象的相对位置可以是( )A、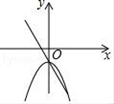 B、
B、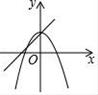 C、
C、 D、
D、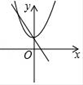 7. 如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′= AA',则折痕DE的长为( )
7. 如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′= AA',则折痕DE的长为( ) A、4 B、3 C、2 D、8. 若A(﹣4,y1),B(﹣1,y2),C(0,y3)为二次函数y=﹣(x+2)2+3的图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2=y3 B、y3=y1<y2 C、y3<y1<y2 D、y1=y2<y39. 如图,城关镇某村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为m米,那么这两树在坡面上的距离AB为( )
A、4 B、3 C、2 D、8. 若A(﹣4,y1),B(﹣1,y2),C(0,y3)为二次函数y=﹣(x+2)2+3的图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2=y3 B、y3=y1<y2 C、y3<y1<y2 D、y1=y2<y39. 如图,城关镇某村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为m米,那么这两树在坡面上的距离AB为( ) A、mcosα B、 C、msinα D、10. 如图,在四边形ABCD中,AB∥CD,点E,F分别为AC,BD的中点,若AB=7,CD=3,则EF的长是( )
A、mcosα B、 C、msinα D、10. 如图,在四边形ABCD中,AB∥CD,点E,F分别为AC,BD的中点,若AB=7,CD=3,则EF的长是( )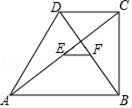 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
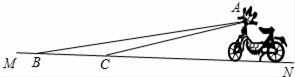
11. 计算: = .12. 在电影票上,如果将“8排4号”记作(4,8),那么(1,5)表示.13. 某广场准备修建一个面积为200平方米的矩形草坪,它的长比宽多2米,设草坪的宽为x米,则可列方程为(不需要化为一般形式).14. 某厂家新开发的一种电动车如图,它的大灯A射出的光线AB、AC与地面MN所夹的锐角分别是8°和10°.大灯A离地面的距离为lm,则该车大灯照亮地面的宽度BC是m.(不考虑其他因素)(参考数据: , , , ).
 15. 已知二次函数y=2x2+2018,当x分别取x1 , x2(x1≠x2)时,函数值相等,则当x取2x1+2x2时,函数值为.
15. 已知二次函数y=2x2+2018,当x分别取x1 , x2(x1≠x2)时,函数值相等,则当x取2x1+2x2时,函数值为.三、解答题
-
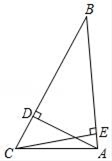
16. 先化简,再求值:(m+n)2+(2m+n)(2m﹣n)﹣m(m+n),其中m、n分别为 的整数部分和小数部分.17. 求证:不论m为任何实数,关于x的方程x2﹣2mx+6m﹣10=0总有两个不相等的实数根.18. 小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,分别为白色、黑色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列出所有可能的结果,并求取出红色水笔和白色橡皮配套的概率.19. 在锐角△ABC中,AD与CE分别是边BC与AB的高,AB=12,BC=16,S△ABC=48,
求:
(1)、角B的度数;(2)、tanC的值.20. 在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(120>x≥60)元,销售量为y套.(1)、求出y与x的函数关系式;(2)、当销售单价为多少元时,月销售额为14000元,此月共盈利多少元.21. 已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求: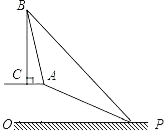 (1)、坡顶A到地面PO的距离;(2)、古塔BC的高度(结果精确到1米).
(1)、坡顶A到地面PO的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
22. 如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.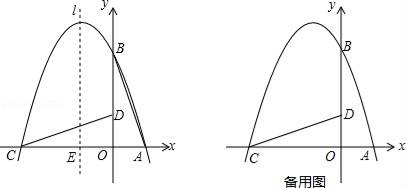 (1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.23. 已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.23. 已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.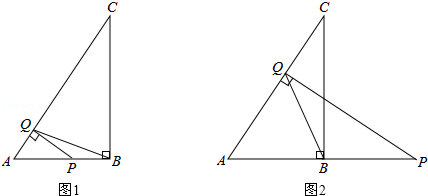 (1)、当点P在线段AB上时,求证:△APQ∽△ABC;(2)、当△PQB为等腰三角形时,求AP的长.
(1)、当点P在线段AB上时,求证:△APQ∽△ABC;(2)、当△PQB为等腰三角形时,求AP的长.