河南省焦作市2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列命题正确的是（）

A、对角线互相垂直的四边形是菱形 B、一组对边相等，另一组对边平行的四边形是平行四边形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分且相等的四边形是正方形

查看试题解析
2. 为了加强视力保护意识，小明要在书房里挂一张视力表。由于书房空间狭小，他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表。如图，如果大视力表中“E”的高度为3.5cm，那么小视力表中相应“E”的高度是（）

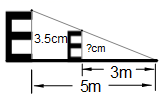A、2.1cm B、2.5cm C、2.3cm D、3cm

查看试题解析
3. 在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，则cosA的值是（　　）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
4. 如图，Rt△AOB的一条直角边OA在 $x$ 轴上，且 $S_{Δ A O B} = 3$ .若某反比例函数图象的一支经过点B，则该反比例函数的解析式为（）

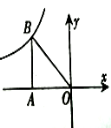A、 $y = \frac{3}{x}$ B、 $y = - \frac{3}{x}$ C、 $y = \frac{6}{x}$ D、 $y = - \frac{6}{x}$

查看试题解析
5. 经过某十字路口的汽车，可能直行，也可能左转或右转。如果这三种可能性大小相同，则经过这个十字路口的两辆汽车一辆左转，一辆右转的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
6. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围是（）

A、 $k < 1$ B、 $k > - 1$ C、 $k < 1$ 且 $k \neq 0$ D、 $k > - 1$ 且 $k \neq 0$

查看试题解析
7. 矩形的一个角的平分线分矩形的一边长为1cm和3cm两部分，则这个矩形的面积是（）

A、4cm² B、6cm² C、12cm² D、4cm²或12cm²

查看试题解析
8. 如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(-1，0).以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的像是△A′B′C.设点B的对应点B′的横坐标是a，则点B的横坐标是（）

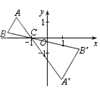A、- $\frac{1}{2} a$ B、 $- \frac{1}{2} (a + 1)$ C、 $- \frac{1}{2} (a + 3)$ D、 $- \frac{1}{2} (a - 1)$

查看试题解析
9. 如果 $sinA = \frac{\sqrt{3}}{2}$ ，那么锐角∠A的度数为（）

A、30° B、45° C、60° D、90°

查看试题解析
10. 如图所示的四棱柱的主视图为（）

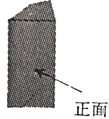A、 B、 C、 D、

查看试题解析

二、填空题

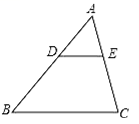
11. 一元二次方程x²=(-4)²的解为 .

查看试题解析
12. 菱形ABCD的周长为52cm，一条对角线的长为24cm，则该菱形的面积为cm² ．

查看试题解析
13. 已知点A（-2， $a$ ），B（1， $b$ ），C（3， $c$ ）都在反比例函数 $y = \frac{k^{2} + 1}{x}$ 的图象上，则 $a$ ， $b$ ， $c$ 间的大小关系为.（用“ $<$ ”连接）

查看试题解析
14. 如图，D，E分别是△ABC的边AB和AC上的动点，且DE∥BC，当DE把△ABC的面积分成1：3的两部分时， $\frac{D E}{B C}$ 的值为.

查看试题解析
15. 在一个不透明的盒子中装有红、黄、蓝三种除颜色外完全相同的小球，其中红球6个，黄球10个，篮球 $a$ 个。若每次将球充分搅匀后，随机摸出一个小球记下颜色后放回盒子里。经过大量的重复试验后发现，摸到红球的频率稳定在30％左右，则 $a$ 的值约为.

查看试题解析

三、解答题

16. 解下列方程.

(1)、 $x - 2 = x (x - 2)$

(2)、 $(x + 8) (x + 1) = - 13$

查看试题解析
17. 有两个信封，每个信封内各装有四张完全相同的卡片，其中一个信封内的四张卡片上分别写有1，2，3，4四个数，另一个信封内的四张卡片上分别写有5，6，7，8四个数.甲，乙两人商定了一个游戏，规则是：从这两个信封中各随机抽取一张卡片，然后把卡片上的两个数相乘，如果得到的积大于16，则甲获胜，否则乙获胜.

(1)、请你通过列表（或画树状图）计算甲获胜的概率；

(2)、你认为这个游戏公平吗？为什么？

查看试题解析
18. 如图，在Rt△ABC中，∠ACB=90°，AC的垂直平分线EF交AC于点D，交AB于点F，且CE=BF.

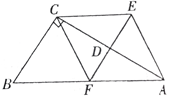(1)、求证：四边形AECF是菱形；

(2)、当∠BAC的度数为多少时，四边形AECF是正方形.

查看试题解析
19. 如图，路灯P距地面8m（即图中OP为8m），身高1.6m的小明从点A处沿AO所在直线行走14m到达点B，求影长BD比AC缩短了多少米？

查看试题解析
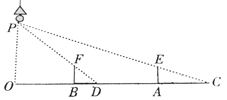20. 如图，在平面直角坐标系中，一次函数 $y_{1} = k_{1} x + b$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点A、B两点，与 $x$ 轴交于点D，过点B作BC $⊥$ $x$ 轴于点C，点O是线段DC的中点， $B D = 2 \sqrt{5}$ ， $\cos ∠ B D C = \frac{\sqrt{5}}{5}$ .

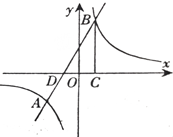(1)、求该反比例函数和一次函数的解析式；

(2)、直接写出当 $x$ 为何值时， $y_{1}$ ≥ $y_{2}$ .

查看试题解析
21. 某花卉种植基地准备围建一个面积为100平方米的矩形苗圃园园种植玫瑰花，其中一边靠墙，另外三边用29米长的篱笆围成.已知墙长为18米，为方便进入，在墙的对面留出1米宽的门（如图所示），求这个苗圃园垂直于墙的一边长为多少米？

查看试题解析
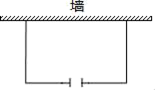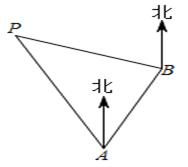22. 一货轮在A处测得灯塔P在货轮的北偏西23°的方向上，随后货轮以80海里/时的速度按北偏东30°的方向航行，1小时后到达B处，此时又测得灯塔P在货轮的北偏西68°的方向上，求此时货轮距灯塔P的距离PB.（参考数据： $\sin 53 ° \approx \frac{4}{5}$ ， $\cos 53 ° \approx \frac{3}{5}$ ， $\tan 53 ° \approx \frac{4}{3}$ ）

查看试题解析
23.

(1)、问题发现：如图①，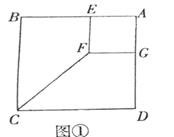

正方形AEFG的两边分别在正方形ABCD的边AB和AD上，连接CF.

①写出线段CF与DG的数量关系；

②写出直线CF与DG所夹锐角的度数.

(2)、拓展探究：
如图②，

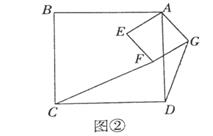
将正方形AEFG绕点A逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明.

(3)、问题解决
如图③，

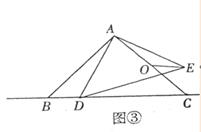
△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O为AC的中点.若点D在直线BC上运动，连接OE，则在点D的运动过程中，线段OE的长的最小值.（直接写出结果）

查看试题解析