河南平顶山市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 在阳光的照射下,一块三角板的投影不会是( )A、线段 B、与原三角形全等的三角形 C、变形的三角形 D、点2. 菱形的两条对角线长分别为6与8,则此菱形的面积为( )A、48 B、20 C、14 D、243. 一元二次方程 配方后化为( )A、 B、 C、 D、4. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形5. 在一个不透明的盒子里,装有5个黑球和若干个白球,这些球除颜色外都相同,将其摇匀后从中随机摸出一个球,记下颜色后再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,请估计盒子中白球的个数是( )A、10个 B、15个 C、20个 D、25个6. 如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
 A、 B、 C、 D、7. 若点 , 在反比例函数 的图象上, ,则 、 的大小关系为A、 B、 C、 D、8. 将进货单价为40元的商品按50元出售时,售出500个,经市场调查发现:该商品每涨价1元,其销量减少10个,为了赚8000元,则售价应定为A、60元 B、80元 C、60元或80元 D、70元9. 反比例函数 在第一象限的图象如图,则k的值有可能是
A、 B、 C、 D、7. 若点 , 在反比例函数 的图象上, ,则 、 的大小关系为A、 B、 C、 D、8. 将进货单价为40元的商品按50元出售时,售出500个,经市场调查发现:该商品每涨价1元,其销量减少10个,为了赚8000元,则售价应定为A、60元 B、80元 C、60元或80元 D、70元9. 反比例函数 在第一象限的图象如图,则k的值有可能是 A、4 B、2 C、 D、1
A、4 B、2 C、 D、1二、填空题
-
10. 方程x2=3x的根是 .11. 某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为。
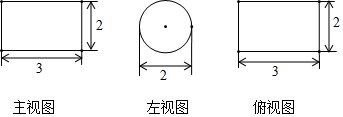 12. 李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生,则小红和小丽同时被抽中的概率是 .
12. 李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生,则小红和小丽同时被抽中的概率是 .
13. 如图,点A是反比例函数图象上的一点,过点A作 轴于点B,点P在x轴上,若 的面积为2,则该反比例函数的解析式为.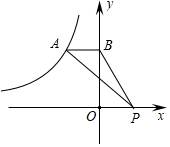 14. 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE=.
14. 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE=.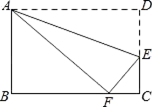
三、解答题
-
15. 按要求解下列一元二次方程(1)、 (公式法)(2)、 (提公因式法)16. 已知关于x的一元二次方程(1)、判断该一元二次方程根的情况.(2)、已知该一元二次方程的一根为 ,求k的值.17. 有三张正面分别标有数字 ,2,4的不透明卡片,它们除数字外都相同;现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记住数字;(1)、若把抽出的卡片放回,洗匀后,再从三张卡片中随机抽出一张,记住数字 试用列表或树状图的方法,求两次抽取的卡片上的数字为一正数、一负数的概率.(2)、若不把抽出的卡片放回,再从剩余两张卡片中随机抽出一张,直接写出两次抽取卡片上的数字为一正数、一负数的概率.18. 如图,学校平房的窗外有一路灯AB,路灯光能通过窗户CD照到平房内EF处;经过测量得:窗户距地面高 ,窗户高度 , , ;求路灯AB的高.
 19. 如图,在 中, 分别为 的中点, ,延长 交 的延长线于点 ,连接 .
19. 如图,在 中, 分别为 的中点, ,延长 交 的延长线于点 ,连接 .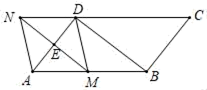 (1)、证明:四边形AMDN是菱形;(2)、若 ,判断四边形 的形状,请直接写出答案.20. 平顶山市某中学开展弘扬传统文化活动,鼓励学生到阅览室借书阅读,并进行统计 校阅览室在2015年图书借阅总量为7500本,2017年图书借阅总量为10800本.(1)、求该学校的图书借阅总量从2015年到2017年连续两年的平均增长率.(2)、已知2017年该校学生借阅图书人数有1350人,预计2018年达到1440人 若2017年至2018年图书借阅总量增长率与2015年到2017年两年的平均增长率相同,那么2018年的人均借阅量比2017年增长 ,求a的值.21. 如图、在矩形OABC中, , 双曲线 与矩形两边BC,AB分别交于E,F两点.
(1)、证明:四边形AMDN是菱形;(2)、若 ,判断四边形 的形状,请直接写出答案.20. 平顶山市某中学开展弘扬传统文化活动,鼓励学生到阅览室借书阅读,并进行统计 校阅览室在2015年图书借阅总量为7500本,2017年图书借阅总量为10800本.(1)、求该学校的图书借阅总量从2015年到2017年连续两年的平均增长率.(2)、已知2017年该校学生借阅图书人数有1350人,预计2018年达到1440人 若2017年至2018年图书借阅总量增长率与2015年到2017年两年的平均增长率相同,那么2018年的人均借阅量比2017年增长 ,求a的值.21. 如图、在矩形OABC中, , 双曲线 与矩形两边BC,AB分别交于E,F两点. (1)、如图一,若E是BC中点,求点F的坐标;(2)、如图二,若将 沿直线EF对折,点B恰好落在x轴上的点D处,求k的值.22. 如图 ,已知点G在正方形ABCD的对角线AC上, ,垂足为点E, ,垂足为点F.
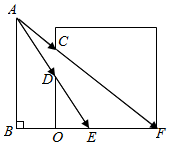
(1)、如图一,若E是BC中点,求点F的坐标;(2)、如图二,若将 沿直线EF对折,点B恰好落在x轴上的点D处,求k的值.22. 如图 ,已知点G在正方形ABCD的对角线AC上, ,垂足为点E, ,垂足为点F.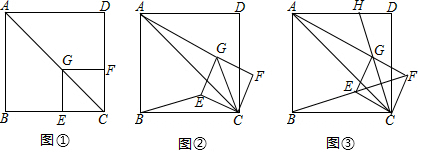 (1)、发现问题:在图 中, 的值为.(2)、探究问题:将正方形CEGF绕点C顺时针方向旋转 角 ,如图 所示,探究线段AG与BE之间的数量关系,并证明你的结论.(3)、解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图 所示,延长CG交AD于点H;若 , ,直接写出BC的长度.
(1)、发现问题:在图 中, 的值为.(2)、探究问题:将正方形CEGF绕点C顺时针方向旋转 角 ,如图 所示,探究线段AG与BE之间的数量关系,并证明你的结论.(3)、解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图 所示,延长CG交AD于点H;若 , ,直接写出BC的长度.