广东省佛山市禅城区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. ﹣3的倒数为( )A、﹣ B、 C、3 D、﹣32. 十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )A、146×107 B、1.46×107 C、1.46×109 D、1.46×10103. 在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )A、1枚 B、2枚 C、3枚 D、任意枚4. 如图,下列图形全部属于柱体的是( )A、
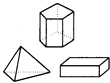 B、
B、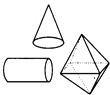 C、
C、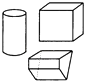 D、
D、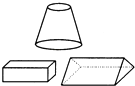 5. “一个数a的3倍与2的和”用代数式可表示为( )A、3(a+2) B、(3+a)a C、2a+3 D、3a+26. 为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计,下列说法正确的是( )A、这种调查方式是普查 B、6000名学生是总体 C、每名学生的数学成绩是个体 D、500名学生是总体的一个样本7. 多项式x2y﹣xy2+3xy﹣1的次数与项数分别是( )A、2,4 B、3,3 C、3,4 D、8,48. 下列四组变形中,属于移项变形的是( )A、由5x+10=0,得5x=﹣10 B、由 ,得x=12 C、由3y=﹣4,得 D、由2x﹣(3﹣x)=6,得2x﹣3+x=69. 下列各式的计算,结果正确的是( )A、3a+2b=5ab B、m2﹣n2=0 C、5x+2x=7x2 D、5xy﹣5yx=010. 观察下列各式:31=3,32=9,33=27,34=81,35=243,36=729,…则:32018的个位数字是( )A、3 B、9 C、7 D、1
5. “一个数a的3倍与2的和”用代数式可表示为( )A、3(a+2) B、(3+a)a C、2a+3 D、3a+26. 为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计,下列说法正确的是( )A、这种调查方式是普查 B、6000名学生是总体 C、每名学生的数学成绩是个体 D、500名学生是总体的一个样本7. 多项式x2y﹣xy2+3xy﹣1的次数与项数分别是( )A、2,4 B、3,3 C、3,4 D、8,48. 下列四组变形中,属于移项变形的是( )A、由5x+10=0,得5x=﹣10 B、由 ,得x=12 C、由3y=﹣4,得 D、由2x﹣(3﹣x)=6,得2x﹣3+x=69. 下列各式的计算,结果正确的是( )A、3a+2b=5ab B、m2﹣n2=0 C、5x+2x=7x2 D、5xy﹣5yx=010. 观察下列各式:31=3,32=9,33=27,34=81,35=243,36=729,…则:32018的个位数字是( )A、3 B、9 C、7 D、1二、填空题
-
11. 比较大小:﹣8﹣9(填“>”、“=”或“<“).12. 在公式s=s0+vt中,已知s=100,s0=25,v=10,则t= .13. 在半径为6cm的圆中,60°的圆心角所对的扇形面积等于cm2(结果保留π).14. 如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=
 15. 如图,小红将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?设正方形边长为xcm,则可列方程为 .
15. 如图,小红将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?设正方形边长为xcm,则可列方程为 . 16. 一个几何体由若干大小相同的小立方块搭成,如图所示的分别是从它的正面、左面看到的图形,则搭成该几何体最多需要个小立方块.
16. 一个几何体由若干大小相同的小立方块搭成,如图所示的分别是从它的正面、左面看到的图形,则搭成该几何体最多需要个小立方块.
三、解答题
-
17. 计算:(﹣1)4﹣|﹣3|×[2﹣(﹣3)2]18. 解方程: (2x﹣1)+1=6(2x+1)19. 如图,已知四点A、B、C、D),请用尺规作图完成.(保留画图痕迹)

⑴画直线AB;(2)画射线AC;(3)连接BC并延长BC到E,使得CE=AB+BC;(4)在线段BD上取点P,使PA+PC的值最小.
20. 已知:A=2x2+3xy-2x-1,B=-x2+xy-1(1)、求A+2B;(2)、若A+2B的值与x的值无关,求y的值.21. 小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟. (1)、以小明家为原点、向东为正方向,用1个单位长度表示1km , 在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;(2)、用点C表示出学校的位置;(3)、求小彬家与学校之间的距离.22. 某校为了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A , B , C , D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(1)、以小明家为原点、向东为正方向,用1个单位长度表示1km , 在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;(2)、用点C表示出学校的位置;(3)、求小彬家与学校之间的距离.22. 某校为了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A , B , C , D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
 (1)、计算D级的学生人数,并把条形统计图补充完整;(2)、计算扇形统计图中A级所在的扇形的圆心角度数:(3)、若该校七年级有600名学生,请估计体育测试中B级学生人数约为多少人?23. 请根据图中提供的信息,回答下列问题:
(1)、计算D级的学生人数,并把条形统计图补充完整;(2)、计算扇形统计图中A级所在的扇形的圆心角度数:(3)、若该校七年级有600名学生,请估计体育测试中B级学生人数约为多少人?23. 请根据图中提供的信息,回答下列问题: (1)、一个水瓶与一个水杯分别是多少元?(2)、甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买5个水瓶和20个水杯,请问选择哪家商场更合算?请说明理由.24. 如图1,点O为直线AB上一点,过点O作射线OC , 使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)、一个水瓶与一个水杯分别是多少元?(2)、甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买5个水瓶和20个水杯,请问选择哪家商场更合算?请说明理由.24. 如图1,点O为直线AB上一点,过点O作射线OC , 使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方. (1)、在图1中,∠AOC=°,∠MOC=°;(2)、将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;(3)、将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.25. 如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动.
(1)、在图1中,∠AOC=°,∠MOC=°;(2)、将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;(3)、将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.25. 如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动. (1)、设运动时间为t(t>0)秒,数轴上点B表示的数是 , 点P表示的数是(用含t的代数式表示);(2)、若点P、Q同时出发,求:①当点P运动多少秒时,点P与点Q相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
(1)、设运动时间为t(t>0)秒,数轴上点B表示的数是 , 点P表示的数是(用含t的代数式表示);(2)、若点P、Q同时出发,求:①当点P运动多少秒时,点P与点Q相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?