河南省洛阳市2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列说法中正确的是（　　）

A、“任意画出一个等边三角形，它是轴对称图形”是必然事件 B、任意掷一枚质地均匀的硬币20次，正面向上的一定是10次 C、“概率为0.00001的事件”是不可能事件 D、“任意画出一个平行四边形，它是中心对称图形”是随机事件

查看试题解析
3. 对于二次函数y＝4（x+1）（x﹣3）下列说法正确的是（　　）

A、图象开口向下 B、与x轴交点坐标是（1，0）和（﹣3，0） C、x＜0时，y随x的增大而减小 D、图象的对称轴是直线x＝﹣1

查看试题解析
4. 如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，若⊙O的直径为4，则弦AB长为（）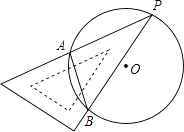

A、2 B、3 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
5. 如图，双曲线y＝ $\frac{k}{x}$ （k＞0）与⊙O在第一象限内交于P、Q两点，分别过P、Q两点向x轴和y轴作垂线，已知点P坐标为（1，3），则图中阴影部分的面积为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，在宽为20米、长为32米的矩形地面上修筑同样宽的道路（图中阴影部分），余下部分种植草坪.要使草坪的面积为540平方米，设道路的宽x米.则可列方程为（　　）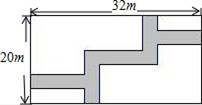

A、32×20﹣32x﹣20x＝540 B、（32﹣x）（20﹣x）＝540 C、32x+20x＝540 D、（32﹣x）（20﹣x）+x²＝540

查看试题解析
7.
如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（）

A、（2，5） B、（5，2） C、（4， $\frac{5}{2}$ ） D、（ $\frac{5}{2}$ ，4）

查看试题解析
8. 若二次函数y＝x²﹣mx的对称轴是x＝﹣3，则关于x的方程x²+mx＝7的解是（　　）

A、x₁＝0，x₂＝6 B、x₁＝1，x₂＝7 C、x₁＝1，x₂＝﹣7 D、x₁＝﹣1，x₂＝7

查看试题解析
9. 某校校园内有一个大正方形花坛，如图甲所示，它由四个边长为3米的小正方形组成，且每个小正方形的种植方案相同．其中的一个小正方形ABCD如图乙所示，DG=1米，AE=AF=x米，在五边形EFBCG区域上种植花卉，则大正方形花坛种植花卉的面积y与x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 用配方法解方程x²﹣8x+2＝0，则方程可变形为（）

A、（x﹣4）²＝5 B、（x+4）²＝21 C、（x﹣4）²＝14 D、（x﹣4）²＝8

查看试题解析

二、填空题

11. 方程(n﹣3)x^|n|^﹣¹+3x+3n＝0是关于x的一元二次方程，n＝.

查看试题解析
12. 袋子中装有红、黄、绿三种颜色的小球各一个，从中任意摸出一个放回搅匀，再摸出一个球，则两次摸出的球都是黄色的概率是．

查看试题解析
13. 抛物线 y= -x $^{2}$ + bx + c 的部分图象如图所示，则关于 x 的一元二次方程-x $^{2}$ + bx + c= 0 的解为

查看试题解析
14. 如图，直角 $Δ A B C$ 中， $∠ A = 90^{0}$ ， $∠ B = 30^{0}$ ， $A C = 4$ ，以 $A$ 为圆心， $A C$ 长为半径画四分之一圆，则图中阴影部分的面积是.（结果保留 $π$ ）

查看试题解析
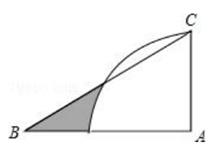15. 如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去….若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₈的坐标为.

查看试题解析

三、解答题

16. 已知关于x的一元二次方程x²+2（k﹣1）x+k²﹣1=0有两个不相等的实数根．

(1)、求实数k的取值范围；

(2)、0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由．

查看试题解析
17. 如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，1）、B（4，0）、C（4，4）.

(1)、按下列要求作图：
①将△ABC向左平移4个单位，得到△A₁B₁C₁；

②将△A₁B₁C₁绕点B₁逆时针旋转得到90°得到△A₂B₂C₂；

(2)、求点C从开始到点C₂的过程中所经过的路径长.

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，DE交AC于点E，且∠A＝∠ADE.

(1)、求证：DE是⊙O的切线；

(2)、若AD＝16，DE＝10，求BC的长.

查看试题解析
19. 如图，在平面直角坐标系中，直线AB与函数y＝ $\frac{k}{x}$ （x＞0）的图象交于点A（m，2），B（2，n）.过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD＝ $\frac{1}{2}$ OC，且△ACD的面积是6，连接BC.

(1)、求m，k，n的值；

(2)、求△ABC的面积.

查看试题解析
20. 为了让学生亲身感受合肥城市的变化，蜀山中学九（1）班组织学生进行“环巢湖一日研学游”活动，某旅行社推出了如下收费标准：（1）如果人数不超过30人，人均旅游费用为100元；（2）如果超过30人，则每超过1人，人均旅游费用降低2元，但人均旅游费用不能低于80元．该班实际共支付给旅行社3150元，问：共有多少名同学参加了研学游活动？

查看试题解析
21. 在等边△AOB中，将扇形COD按图1摆放，使扇形的半径OC、OD分别与OA、OB重合，OA＝OB＝2，OC＝OD＝1，固定等边△AOB不动，让扇形COD绕点O逆时针旋转，线段AC、BD也随之变化，设旋转角为α.（0＜α≤360°）

(1)、当OC $∥$ AB时，旋转角α＝度；

(2)、【发现】线段AC与BD有何数量关系，请仅就图2给出证明.

(3)、【应用】当A、C、D三点共线时，求BD的长.

(4)、【拓展】P是线段AB上任意一点，在扇形COD的旋转过程中，请直接写出线段PC的最大值与最小值.

查看试题解析
22. 如图，已知二次函数y=ax²+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）.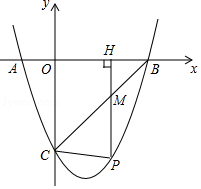

(1)、求这个二次函数的表达式；

(2)、若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC.
①求线段PM的最大值；

②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标.

查看试题解析