湖北省宜昌市伍家岗区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 三条高的交点一定在三角形内部的是（）

A、任意三角形 B、锐角三角形 C、直角三角形 D、纯角三角形

查看试题解析
2. 下列运算正确的是（）

A、 $a^{6} \div a^{3} = a^{3} (a \neq 0)$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $3 a + 2 a = 5 a^{2}$ D、 ${(a^{3})}^{2} = a^{9}$

查看试题解析
3. 用直尺和圆规作一个角的平分线如图所示，说明∠AOC＝∠BOC的依据是（）．

A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等

查看试题解析
4. 如图，将△ABC沿直线DE折叠后，使点B与点A重合，已知AC=5cm，△ADC的周长为14cm，则BC的长为（）

A、8cm B、9cm C、10cm D、11cm

查看试题解析
5. 若分式 $\frac{x^{2} - 4}{(x - 2) (x - 1)}$ 的值为零,则 $x$ 的值是（）

A、2或-2 B、2 C、-2 D、4

查看试题解析
6. 计算 $\frac{{(a + b)}^{2} - {(a - b)}^{2}}{2 a b}$ 的结果为（）

A、 $\frac{a^{2} + b^{2}}{a b}$ B、 $2 a b$ C、 $1$ D、 $2$

查看试题解析
7. 下列各式中不能用完全平方公式分解因式的是（　　）

A、x²+2x+1 B、x²﹣2xy+y² C、﹣x²﹣2x+1 D、x²﹣x+0.25

查看试题解析
8. 若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为（）

A、4cm B、6cm C、8cm D、4cm或8cm

查看试题解析
9. 如果把分式 $\frac{x + y}{x - y}$ 中的 $x$ 和 $y$ 都扩大为原来的10倍,那么分式的值（）

A、扩大10倍 B、缩小10倍 C、是原来的100倍 D、不变

查看试题解析
10. 在正方形网格中， $∠ A O B$ 的位置如图所示，到 $∠ A O B$ 的两边距离相等的点应是（）

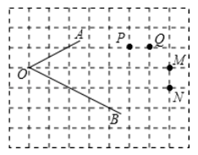A、点M B、点Q C、点P D、点N

查看试题解析
11. 如图所示，△ABC是等边三角形，且BD＝CE，∠1＝15°，则∠2的度数为（　　）

A、15° B、30° C、45° D、60°

查看试题解析
12. 一个多边形的每一个外角都等于72°,则这个多边形的内角和等于（）

A、360° B、540° C、720° D、900°

查看试题解析
13. 如图，小明书上的三角形被墨迹遮挡了一部分，测得两个角的度数为32°、74°，于是他很快判断这个三角形是（）

A、等边三角形 B、等腰三角形 C、直角三角形 D、钝角三角形

查看试题解析
14. 如图，七边形ABCDEFG中，AB、ED的延长线交于点O，若∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析

二、解答题

15. 已知: $a + b = 8 ， a b = 6.$

(1)、求 ${(a + b)}^{2}$ 的值；

(2)、求 $a^{2} + b^{2}$ 的值.

查看试题解析
16. 如图，AE∥BD，∠1=115°，∠2=35°，求∠C的度数.

查看试题解析
17. 如图，已知AB $∥$ CF，AC和DF交于点E，ED=EF，若AB=15cm，CF=11cm，求BD的长.

查看试题解析
18. 计算：（1﹣ $\frac{1}{m - 2}$ ）÷ $\frac{m - 3}{2 m - 4}$ .

查看试题解析
19. 解分式方程： $\frac{x - 1}{x + 1} = \frac{1}{x + 2} + 1$

查看试题解析
20. 为进一步普及我市中小学生的法律知识，提升学生法律意识，在2018年12月4日第五个国家宪法日来临之际，我市某区在中小学举行了“学习宪法”知识竞赛活动，各类获奖学生人数的比例情况如图所示，其中获得优胜奖的学生共400名，请结合图中信息，解答下列问题：

(1)、求获得一等奖的学生人数；

(2)、在本次知识竞赛活动中，A，B，C，D四所学校表现突出，现决定从这四所学校中随机选取两所学校举行一场法律知识抢答赛，请用画树状图或列表的方法求恰好选到A，B两所学校的概率.

查看试题解析
21. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同．

(1)、原计划平均每天生产多少台机器？

(2)、若该工厂要在不超过5天的时间，生产1100台机器，则平均每天至少还要再多生产多少台机器？

查看试题解析
22. 将两个大小不同的含30°角的三角板的直角顶点O重合在一起，保持△COD不动，将△AOB绕点O旋转，设射线AB与射线DC交于点F.

(1)、如图①，若∠AOD=120°，
①AB与OD的位置关系.

②∠AFC的度数=.

(2)、如图②当∠AOD=130°，求∠AFC的度数.

(3)、由上述结果，写出∠AOD和∠AFC的关系.

(4)、如图③，作∠AFC、∠AOD的角平分线交于点P，求∠P的度数.

查看试题解析
23. 如图，在平面直角坐标系中，A（a，0），B（b，0），C（b，-2a）.且 $\sqrt{a b + 4}$ +|b-l|=0.CD $∥$ AB，AD $∥$ BC

(1)、直接写出B、C、D各点的坐标：B、C、D；

(2)、如图1，P（3，10），点E，M在四边形ABCD的边上，且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形，请直接写出点E的坐标，并对其中一种情况计算说明；

(3)、如图2，F为y轴正半轴上一动点，过F的直线j $∥$ x轴，BH平分∠FBA交直线j于点H.G为BF上的点，且∠HGF=∠FAB，F在运动中FG的长度是否发生变化？若变化，求出变化范围；若不变，求出定值.

查看试题解析