湖北省武汉市青山区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（　　）

A、 B、 C、 D、

查看试题解析
2. 无论x取什么值，下列分式总有意义的是（）

A、 $\frac{2 + x}{x}$ B、 $\frac{x}{x^{2} + 1}$ C、 $\frac{3 x}{{(x - 1)}^{2}}$ D、 $\frac{x^{2} + 1}{| x |}$

查看试题解析
3. 下列等式从左到右的变形，属于因式分解的是（　　）

A、a（x﹣y）=ax﹣ay B、x²+2x+1=x（x+2）+1 C、（x+1）²=x²+2x+1 D、x²﹣x=x（x﹣1）

查看试题解析
4. 已知被除式是x³+3x²﹣1，商式是x ，余式是﹣1，则除式是（　　）

A、x²+3x﹣1 B、x²+3x C、x²﹣1 D、x²﹣3x+1

查看试题解析
5. 如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）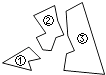

A、带①去 B、带②去 C、带③去 D、带①和②去

查看试题解析
6. 下列各式从左到右的变形正确的是（　　）

A、 $\frac{{(- a + b)}^{2}}{{(a - b)}^{2}}$ ＝1 B、 $\frac{- a - 1}{- a^{2} + 8} = \frac{a - 1}{a^{2} + 8}$ C、 $\frac{x^{2} + y^{2}}{x + y}$ ＝x+y D、 $\frac{0.5 + 2 y}{- 0.1 + x} = \frac{5 + 2 y}{1 + x}$

查看试题解析
7. 甲、乙两船从相距300km的A，B两地同时出发相向而行，甲船从A地顺流航行180km时与从B地逆流航行的乙船相遇，水流的速度为6km/h，若甲、乙两船在静水中的速度均为xkm/h，则求两船在静水中的速度可列方程为（　　）

A、 $\frac{180}{x + 6}$ = $\frac{120}{x - 6}$ B、 $\frac{180}{x - 6}$ = $\frac{120}{x + 6}$ C、 $\frac{180}{x + 6}$ = $\frac{120}{x}$ D、 $\frac{180}{x}$ = $\frac{120}{x - 6}$

查看试题解析
8. 如图，A，B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC是等腰三角形，则符合条件是点C共有（　　）个.

A、8 B、9 C、10 D、11

查看试题解析
9. 一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是（）

A、3 B、4 C、6 D、12

查看试题解析

二、填空题

10. 当x=时，分式 $\frac{x^{2} - 9}{x + 3}$ 的值为零.

查看试题解析
11. 计算：（ $\frac{\sqrt{2}}{2}$ ）⁰﹣1= ．

查看试题解析
12. 计算4y·（-2xy²）的结果等于.

查看试题解析
13. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)}$ = $\frac{A}{x - 1}$ + $\frac{B}{x - 2}$ ，则实数A= ．

查看试题解析
14. 如图中的四边形均为长方形，根据图形，写出一个正确的等式：.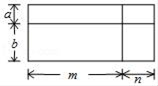

查看试题解析
15. 在等边三角形ABC中，点F是线段AC上一点，点E是线段BC上一点，BF与AE交于点H，∠BAE＝∠FBC，AG⊥BF，∠GAF：∠BEA＝1：10，则∠BAE＝°.

查看试题解析

三、解答题

16. 计算:

(1)、(3x+1)(x+2)

(2)、 $\frac{1}{2 p + 3}$ + $\frac{1}{2 p - 3}$

查看试题解析
17. 已知a+b＝2，ab＝2，求 $\frac{1}{2}$ a³b+a²b²+ $\frac{1}{2}$ ab³的值.

查看试题解析
18. 先化简，再求值：（ $\frac{x^{2} - 2 x + 1}{x^{2} - x}$ + $\frac{x^{2} - 4}{x^{2} + 2 x}$ ）÷ $\frac{1}{x}$ ，且x为满足﹣3＜x＜2的整数．

查看试题解析
19. 为响应珠海环保城市建设，我市某污水处理公司不断改进污水处理设备，新设备每小时处理污水量是原系统的1.5倍，原来处理1200m³污水所用的时间比现在多用10小时．

(1)、原来每小时处理污水量是多少m²？

(2)、若用新设备处理污水960m³ ，需要多长时间？

查看试题解析
20. 如图，BC⊥CD，∠1＝∠2＝∠3，∠4＝60°，∠5＝∠6.

(1)、CO是△BCD的高吗？为什么？

(2)、求∠5、∠7的度数.

查看试题解析
21. 从甲地到乙地有两条公路：一条是全长400千米的普通公路，一条是全长360千米的高速公路.某客车在高速公路上行驶的平均速度比在普通公路上行驶的平均速度快50千米/时，从甲地到乙地由高速公路上行驶所需的时间比普通公路上行驶所需的时间少6小时.求该客车在高速公路上行驶的平均速度.

查看试题解析
22. 如图所示，D是等边三角形ABC外一点，DB＝DC，∠BDC＝120°，点E，F分别在AB，AC上.

(1)、求证：AD是BC的垂直平分线.

(2)、若ED平分∠BEF，求证：FD平分∠EFC.

(3)、在（2）的条件下，求∠EDF的度数.

查看试题解析
23. 如图，已知△ABC中，∠ACB＝90°，AC＝8，cosA＝ $\frac{4}{5}$ ，D是AB边的中点，E是AC边上一点，联结DE，过点D作DF⊥DE交BC边于点F，联结EF.

(1)、如图1，当DE⊥AC时，求EF的长；

(2)、如图2，当点E在AC边上移动时，∠DFE的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出∠DFE的正切值；

(3)、如图3，联结CD交EF于点Q，当△CQF是等腰三角形时，请直接写出BF的长.

查看试题解析