湖北省鄂州市梁子湖区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是A、 B、 C、 D、3. 函数y= + 中自变量x的取值范围是( )
2. 下列运算正确的是A、 B、 C、 D、3. 函数y= + 中自变量x的取值范围是( )
A、x≤2 B、x≤2且x≠1 C、x<2且x≠1 D、x≠14. 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A、k B、 C、 D、5. 如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )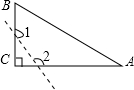 A、90° B、135° C、270° D、315°6. 空气质量检测数据 是值环境空气中,直径小于等于 微米的颗粒物,已知1微米 米, 微米用科学记数法可表示为 米.A、 B、 C、 D、7. 若x2+2(m﹣3)x+16是完全平方式,则m的值等于( )A、3 B、﹣5 C、7 D、7或﹣18. 如图,DE是△ABC中AC边的垂直平分线。BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米
A、90° B、135° C、270° D、315°6. 空气质量检测数据 是值环境空气中,直径小于等于 微米的颗粒物,已知1微米 米, 微米用科学记数法可表示为 米.A、 B、 C、 D、7. 若x2+2(m﹣3)x+16是完全平方式,则m的值等于( )A、3 B、﹣5 C、7 D、7或﹣18. 如图,DE是△ABC中AC边的垂直平分线。BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米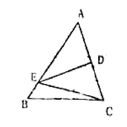 A、16 B、18 C、26 D、289. 如图,在 中, 和 的平分线相交于点O,过O点作 交AB于点E,交AC于点F,过点O作 于D,下列四个结论.
A、16 B、18 C、26 D、289. 如图,在 中, 和 的平分线相交于点O,过O点作 交AB于点E,交AC于点F,过点O作 于D,下列四个结论.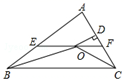
点O到 各边的距离相等 设 , ,则 ,正确的结论有 个.
A、1个 B、2个 C、3个 D、4个10. 如图, 和 都是等腰直角三角形,且 , ,O为AC中点 若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值为 A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
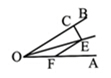
11. 已知正n边形的每一个内角为150°,则n=.12. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= .
 13. 若a+b=5,ab=3,则3a2+3b2=.14. 分解因式: .15. 关于x的分式方程 的解为正数,则m的取值范围是.16. 在等边△ABC所在平面内有点P,且使得△ABP,△ACP,△BCP均为等腰三角形,则符合条件的点P共有个.
13. 若a+b=5,ab=3,则3a2+3b2=.14. 分解因式: .15. 关于x的分式方程 的解为正数,则m的取值范围是.16. 在等边△ABC所在平面内有点P,且使得△ABP,△ACP,△BCP均为等腰三角形,则符合条件的点P共有个.三、解答题
-
17. 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
 (1)、若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;(2)、探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.18. 计算:(1)、(2)、19.(1)、解方程: ;(2)、化简: .20. 如图在平面直角坐标系中, 各顶点的坐标分别为: , ,
(1)、若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;(2)、探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.18. 计算:(1)、(2)、19.(1)、解方程: ;(2)、化简: .20. 如图在平面直角坐标系中, 各顶点的坐标分别为: , , (1)、在图中作 使 和 关于x轴对称;(2)、写出点 的坐标;(3)、求 的面积.21. 仔细阅读下面例题,解答问题:
(1)、在图中作 使 和 关于x轴对称;(2)、写出点 的坐标;(3)、求 的面积.21. 仔细阅读下面例题,解答问题:例题:已知二次三项式 有一个因式是 ,求另一个因式以及m的值.
解:设另一个因式为 ,得
则
.
解得: ,
另一个因式为 ,m的值为
问题:仿照以上方法解答下面问题:
已知二次三项式 有一个因式是 ,求另一个因式以及k的值.
22. 如图, 为等边三角形, ,AD、BE相交于点P, 于Q, , . (1)、求证: ;(2)、求AD的长.23. 济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.(1)、求乙工程队单独完成这项工作需要多少天?(2)、因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?24. 已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足 +|a−3 |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)、求证: ;(2)、求AD的长.23. 济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.(1)、求乙工程队单独完成这项工作需要多少天?(2)、因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?24. 已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足 +|a−3 |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E. (1)、求∠OAB的度数;(2)、设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;(3)、设AB=6,若∠OPD=45°,求点D的坐标.
(1)、求∠OAB的度数;(2)、设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;(3)、设AB=6,若∠OPD=45°,求点D的坐标.