河南省南阳市南召县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、﹣2 B、2 C、﹣4 D、42. 下列计算正确的是( )A、4a2 ÷2a2=2a2 B、﹣( a3 )2=a6 C、(﹣2a)(﹣a)=2a2 D、(a﹣b)(﹣a﹣b)=a2﹣b23. 某单位有职工100名,按他们的年龄分成8组,在40~42(岁)组内有职工32名,那么这个小组的频率是( )A、0.12 B、0.38 C、0.32 D、324. 若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形5. 由 ,则c的值为( )A、2 B、3 C、 D、6. 如图,在 中, ,AE是 的平分线,点D是AE上的一点,则下列结论错误的是
 A、 B、 ≌ C、 ≌ D、7. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A、 B、 ≌ C、 ≌ D、7. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )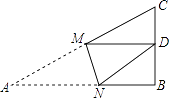 A、 B、 C、4 D、58. 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
A、 B、 C、4 D、58. 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( ) A、25人 B、35人 C、40人 D、100人9. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、25人 B、35人 C、40人 D、100人9. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
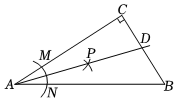
A、15 B、30 C、45 D、6010. 如图,在 的网格中,每个网格线的交点称为格点.已知 为两个格点,请在图中再寻找另一个格点 ,使 成为等腰三角形,则满足条件的 点的个数为( )
A、15 B、30 C、45 D、6010. 如图,在 的网格中,每个网格线的交点称为格点.已知 为两个格点,请在图中再寻找另一个格点 ,使 成为等腰三角形,则满足条件的 点的个数为( ) A、10个 B、8个 C、6个 D、4个
A、10个 B、8个 C、6个 D、4个二、填空题
-
11. =.12. 命题“对顶角相等”的逆命题是 命题(填“真”或“假”).13. 已知a+b=3,ab=1,则a2﹣ab+b2=.14. 如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是.
 15. 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上任一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当CE的长为时,△CEB′恰好为直角三角形.
15. 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上任一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当CE的长为时,△CEB′恰好为直角三角形.
三、解答题
-
16. 计算:(﹣3ab2)3÷a2b3×(﹣2ab3c)17. 因式分解:a2+4a(b+c)+4(b+c)2.18. 先化简,再求值:当|x﹣2|+(y+1)2=0时,求[(3x+2y)(3x﹣2y)+(2y+x)(2y﹣3x)]÷4x的值.19. 如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
 (1)、这个梯子的顶端离地面有多高?(2)、如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?20. 某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:老师在课堂上放手让学生提问和表达( )
(1)、这个梯子的顶端离地面有多高?(2)、如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?20. 某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:老师在课堂上放手让学生提问和表达( )A.从不 B.很少 C.有时 D.常常 E.总是
答题的学生在这五个选项中只能选择一项.下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图.
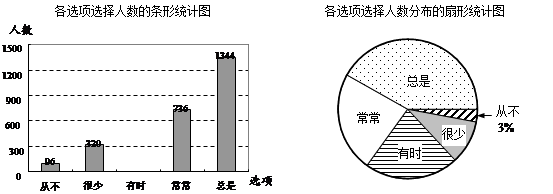
根据以上信息,解答下列问题:
(1)、该区共有名初二年级的学生参加了本次问卷调查;(2)、请把这幅条形统计图补充完整;(3)、在扇形统计图中,“总是”的圆心角为.(精确到度)21. 已知,如图,△ABC中,AB=AC,∠A=36°.(1)、作AB边的垂直平分线,垂足为M,交AC于N,连结BN.(不写作法,保留作图痕迹)(2)、①直接写出∠ABN的度数为;②若BC=12,直接写出BN的长为.
 22. 问题情景:如图1,在等腰直角三角形ABC中∠ACB=90°,BC=a.将AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作△BCD的BC边上的高DE.
22. 问题情景:如图1,在等腰直角三角形ABC中∠ACB=90°,BC=a.将AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作△BCD的BC边上的高DE.易证△ABC≌△BDE,从而得到△BCD的面积为 .
简单应用:如图2,在Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含a的代数式表示△BCD的面积,并说明理由.
 23. 如图1,在四边形ABCD中,AB=AD.∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF= ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
23. 如图1,在四边形ABCD中,AB=AD.∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF= ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系. (1)、思路梳理
(1)、思路梳理将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线. 易证△AFG , 故EF,BE,DF之间的数量关系为;
(2)、类比引申如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC的延长线上,∠EAF= ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)、联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°. 若BD=1,EC=2,则DE的长为.