河南省洛阳市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 若分式 在实数范围内有意义,则实数x的取值范围是( )A、x>﹣2 B、x<﹣2 C、x=﹣2 D、x≠﹣22. 在下列计算中,正确的是( )A、b3•b3=b6 B、x4•x4=x16 C、(﹣2x2)2=﹣4x4 D、3x2•4x2=12x23. 如图,∠AOB=30°,点P在∠AOB的平分线上,PC⊥OB于点C,PD∥OB交OA于点D,若PD=2,PC=( )
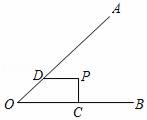 A、1 B、2 C、3 D、44. 下列因式分解正确的是( )A、12a2b﹣8ac+4a=4a(3ab﹣2c) B、﹣4x2+1=(1+2x)(1﹣2x) C、4b2+4b﹣1=(2b﹣1)2 D、a2+ab+b2=(a+b)25. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?( )
A、1 B、2 C、3 D、44. 下列因式分解正确的是( )A、12a2b﹣8ac+4a=4a(3ab﹣2c) B、﹣4x2+1=(1+2x)(1﹣2x) C、4b2+4b﹣1=(2b﹣1)2 D、a2+ab+b2=(a+b)25. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?( )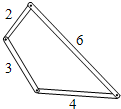 A、5 B、6 C、7 D、106. 计算:a2﹣(b﹣1)2结果正确的是( )A、a2﹣b2﹣2b+1 B、a2﹣b2﹣2b﹣1 C、a2﹣b2+2b﹣1 D、a2﹣b2+2b+17. 分式方程 的解为( )A、x=-2 B、x=-3 C、x=2 D、x=38. 如图,已知点B,E,C,F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是( )
A、5 B、6 C、7 D、106. 计算:a2﹣(b﹣1)2结果正确的是( )A、a2﹣b2﹣2b+1 B、a2﹣b2﹣2b﹣1 C、a2﹣b2+2b﹣1 D、a2﹣b2+2b+17. 分式方程 的解为( )A、x=-2 B、x=-3 C、x=2 D、x=38. 如图,已知点B,E,C,F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是( )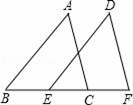 A、AB=DE B、AC=DF C、∠A=∠D D、∠ACB=∠F9. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,则下列结论成立的是( )
A、AB=DE B、AC=DF C、∠A=∠D D、∠ACB=∠F9. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,则下列结论成立的是( )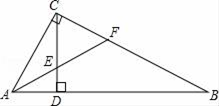 A、EC=EF B、FE=FC C、CE=CF D、CE=CF=EF10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、EC=EF B、FE=FC C、CE=CF D、CE=CF=EF10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )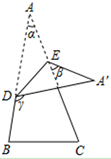 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
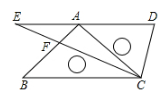
11. 计算:( a3x4﹣0.9ax3)÷ ax3=.12. 一个等腰三角形一边长为3cm,另一边长为7cm,那么这个等腰三角形的周长是cm.13. 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为.
 14. 化简 -a-1 =.15. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为cm.
14. 化简 -a-1 =.15. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为cm.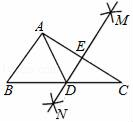
三、解答题
-
16. 解答下列各题:(1)、计算:(y﹣2)(y+5)﹣(y+3)(y﹣3)(2)、分解因式:3x2﹣1217. 化简分式( + )÷ ,并在2,3,4,5这四个数中取一个合适的数作为a的值代入求值.18. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
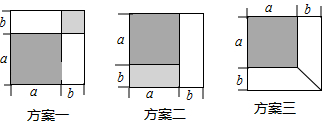
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2 , 对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
(1)、方案二:(2)、方案三:19. 如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).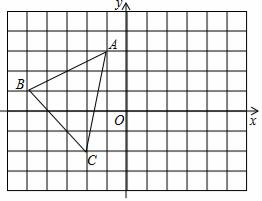 (1)、画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;(2)、求出△ABC的面积.20. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)、画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;(2)、求出△ABC的面积.20. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O. (1)、求证:△AEC≌△BED;(2)、若∠1=40°,求∠BDE的度数.21. 已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)、求证:△AEC≌△BED;(2)、若∠1=40°,求∠BDE的度数.21. 已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.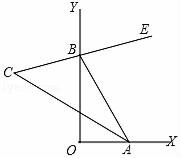 (1)、当∠OAB=40°时,∠ACB=度;(2)、随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.22. 某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.(1)、第一批饮料进货单价多少元?(2)、若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?23. 如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(1)、当∠OAB=40°时,∠ACB=度;(2)、随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.22. 某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.(1)、第一批饮料进货单价多少元?(2)、若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?23. 如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.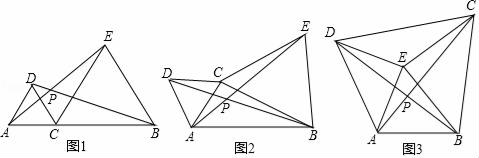 (1)、【观察猜想】
(1)、【观察猜想】①AE与BD的数量关系是;
②∠APD的度数为.
(2)、【数学思考】如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)、【拓展应用】如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,求四边形ABCD的面积.