河南焦作市沁阳市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-30 类型:期末考试
一、单选题
-
1. 下列“QQ表情”中属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式 有意义,则x的取值范围是( )A、x≠0 B、 C、 D、3. 下列各式的变形中,正确的是( )A、(-x-y)(-x+y)=x2-y2 B、 -x= C、x2-4x+3=(x-2)2+1 D、x÷(x2+x)= +14. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )A、7 B、10 C、35 D、705. 在平面直角坐标中,已知点 在第二象限,则点P关于直线 直线m上各点的横坐标都是 对称的点的坐标是A、 B、 C、 D、6. 要使多项式(x2+px+2)(x-q)不含x的二次项,则p与q的关系是( )A、相等 B、互为相反数 C、互为倒数 D、乘积为-17. 将一个四边形截去一个角后,它不可能是( )
2. 若分式 有意义,则x的取值范围是( )A、x≠0 B、 C、 D、3. 下列各式的变形中,正确的是( )A、(-x-y)(-x+y)=x2-y2 B、 -x= C、x2-4x+3=(x-2)2+1 D、x÷(x2+x)= +14. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )A、7 B、10 C、35 D、705. 在平面直角坐标中,已知点 在第二象限,则点P关于直线 直线m上各点的横坐标都是 对称的点的坐标是A、 B、 C、 D、6. 要使多项式(x2+px+2)(x-q)不含x的二次项,则p与q的关系是( )A、相等 B、互为相反数 C、互为倒数 D、乘积为-17. 将一个四边形截去一个角后,它不可能是( )
A、六边形 B、五边形 C、四边形 D、三角形8. 如图,在 中,已知 ,点D,E分别在AC,AB上,且 , ,那么 的度数是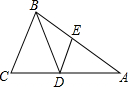 A、 B、 C、 D、9. 如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.
A、 B、 C、 D、9. 如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.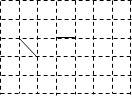 A、1 B、2 C、3 D、410. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A、1 B、2 C、3 D、410. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )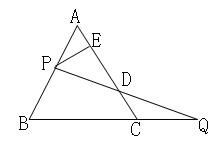 A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
11. 若 , ,则 的值是.12. 如图,已知 的周长是18,OB,OC分别平分 和 , 于D,且 ,则 的面积是.
 13. 若关于x的分式方程 无解,则实数m=.14. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙 若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为.
13. 若关于x的分式方程 无解,则实数m=.14. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙 若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为.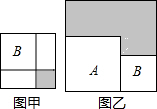 15. 如图,在 中, , , 的平分线与AB的垂直平分线交于点O,将 沿EF折叠,若点C与点O恰好重合,则 .
15. 如图,在 中, , , 的平分线与AB的垂直平分线交于点O,将 沿EF折叠,若点C与点O恰好重合,则 .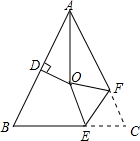
三、解答题
-
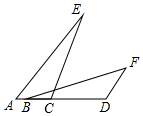
16.(1)、分解因式: .(2)、计算:17. 先化简, ,然后从 的范围内选取一个合适的整数作为x的值代入求值.18. 如图,点A,B,C,D在同一条直线上, , , 求证: .
 19. 尺规作图 保留作图痕迹 :如图,已知直线l及其两侧两点A、B.
19. 尺规作图 保留作图痕迹 :如图,已知直线l及其两侧两点A、B.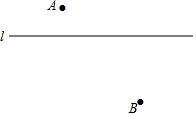
①在直线l上求一点P,使到A、B两点距离之和最短;
②在直线l上求一点Q,使 ;
③在直线l上求一点M,使l平分 .
20. 若关于x的分式方程 的解为正实数,求实数m的取值范围.21. 点P、Q分别是边长为4cm的等边 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是 ,设运动时间为t秒.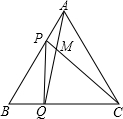 (1)、连接AQ、CP交于点M,则在P、Q运动的过程中, 变化吗:若变化,则说明理由,若不变,则求出它的度数;(2)、连接PQ,
(1)、连接AQ、CP交于点M,则在P、Q运动的过程中, 变化吗:若变化,则说明理由,若不变,则求出它的度数;(2)、连接PQ,当 秒时,判断 的形状,并说明理由;
当 时,则 秒 直接写出结果
22. 在“双十二”期间, 两个超市开展促销活动,活动方式如下:超市:购物金额打9折后,若超过2000元再优惠300元;
超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在 两个超市的标价相同,根据商场的活动方式:
(1)、若一次性付款4200元购买这种篮球,则在 商场购买的数量比在 商场购买的数量多5个,请求出这种篮球的标价;(2)、学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)23. 如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点 点 且a、b满足 .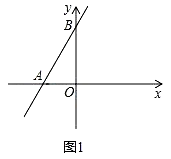
(1)、 ; .(2)、点P在直线AB的右侧,且 ,若点P在x轴上,则点P的坐标为;
若 为直角三角形,求点P的坐标;
(3)、如图2,在(2)的条件下, 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接 求证: 提示:过点P作 交x轴于