河南省许昌市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在△ABC中，∠A＝80°，点D在BC的延长线上，∠ACD＝145°，则∠B是（）

A、45° B、55° C、65° D、75°

查看试题解析
3. 若分式 $\frac{x + 3}{x - 3}$ 的值为0，则 $x$ 的值为（　　）

A、0 B、-3 C、3 D、3或-3

查看试题解析
4. 若正多边形的一个外角是 $60 °$ ，则该正多边形的内角和为（　　）

A、 $360 °$ B、 $720 °$ C、 $900 °$ D、 $1080 °$

查看试题解析
5. 如图，已知BD平分∠ABC，则不一定能使△ABD≌△CBD的条件是（）

A、∠A=∠C B、∠ADB=∠CDB C、AB=CB D、AD=CD

查看试题解析
6. 下列运算正确的是（）

A、 $a^{4} \div a^{3} = a$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{4} - a^{3} = a$ D、 $a^{2} + a^{3} = a^{5}$

查看试题解析
7. 如图，在△ABC中，AB=8，BC=6，AC=5，点D在AC上，连结BD，将△ABC沿BD折叠后，若点C恰好落在AB边上的点E处，则△ADE的周长为（）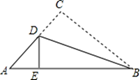

A、5 B、6 C、7 D、8

查看试题解析
8. 如图，在Rt△ABC中，∠C=90°，点D为AB边中点， DE⊥AB，并与AC边交于点E.如果∠A=15°，BC= $\sqrt{2}$ ，那么AE等于（　　）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析
9. 在幼发拉底河岸的古代庙宇图书馆遗址里，曾经发掘出大量的黏土板，美索不达米亚人在这些黏土板上刻出来乘法表、加法表和平方表.用这些简单的平方表，他们很快算出两数的乘积.例如：对于95×103，美索不达米亚人这样计算：第一步：（103+95）÷2=99；第二步：（103-95）÷2=4；第三步：查平方表，知99的平方是9801；第四步：查平方表，知4的平方是16；第五步：9801-16=9785=95×103. 请结合以上实例，设两因数分别为a和 b,写出蕴含其中道理的整式运算（）

A、 $\frac{{(a + b)}^{2} - {(a - b)}^{2}}{2} = a b$ B、 $\frac{{(a + b)}^{2} - (a^{2} + b^{2})}{2} = a b$ C、 ${(\frac{a + b}{2})}^{2} + {(\frac{a - b}{2})}^{2} = a b$ D、 ${(\frac{a + b}{2})}^{2} - {(\frac{a - b}{2})}^{2} = a b$

查看试题解析
10. 在矩形ABCD中，AD=3，AB=2，现将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂.则S₁﹣S₂的值为（　　）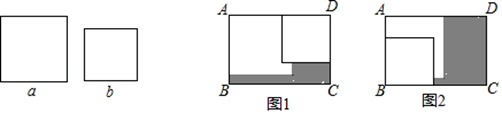

A、-1 B、b﹣a C、-a D、﹣b

查看试题解析

二、填空题

11. 点A(2，－3)关于x轴对称的点的坐标是．

查看试题解析
12. 计算： $π^{0} + 2^{- 2} - {(\frac{1}{2})}^{- 1}$ =.

查看试题解析
13. 已知一等腰三角形的两边长为3cm和7cm，则其腰长为cm.

查看试题解析
14. 已知 $\frac{1}{x} - \frac{1}{y} = 2$ ，则代数式 $\frac{2 x + x y - 2 y}{x - x y - y}$ 的值是.

查看试题解析
15. 如图，在△ABC中，AB = AC = 8，S_△_ABC= 16，点P为角平分线AD上任意一点，PE⊥AB，连接PB，则PB+PE的最小值为.

查看试题解析
16. 如图，在Rt△ABC中， AB＝AC，点D为BC中点，点E在AB边上，连接DE，过点D作DE的垂线，交AC于点F.下列结论：①△BDE≌△ADF；②AE＝CF；③BE+CF＝EF；④S_四边形_AEDF＝ $\frac{1}{2}$ AD² ，其中正确的结论是（填序号）.

查看试题解析

三、解答题

17.

(1)、计算： ${(x + 1)}^{2} - x (x - 1)$

(2)、因式分解： $a^{3} - 4 a b^{2}$ .

查看试题解析
18. 已知：在 $Δ A B C$ 中， $A B = A C$ ， $D$ 为 $A C$ 的中点， $D E ⊥ A B$ ， $D F ⊥ B C$ ，垂足分别为点 $E ， F$ ，且 $D E = D F$ .求证： $Δ A B C$ 是等边三角形.

查看试题解析
19. 如图，在边长为1的小正方形网格中，点A，B，C均落在格点上.

(1)、直接写出△ABC的面积.

(2)、画出△ABC关于直线 $l$ 的轴对称图形△A₁B₁C₁.

(3)、判断△A₁B₁C₁的形状，并说明理由.

查看试题解析
20. 先化简： $（ a - \frac{2 a - 1}{a}) \div \frac{1 - a^{2}}{a^{2} + a}$ ，然后从0，1，2中选一个你认为合适的a值，代入求值.

查看试题解析
21. 如图，在平面直角坐标系第一象限中有一点B. 要求：用尺规作图作一条直线AC，使它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC全等.

(1)、小明的作法是：过B点分别向x 轴、y 轴作垂线，垂足为A、C，连接A、C，则直线AC即为所求.请你帮助小明在图中完成作图（保留作图痕迹）；

(2)、请在图中再画出另一条满足条件的直线AC，并说明理由.

查看试题解析
22. 小丽和小颖相约周末到时代广场看电影，她们的家分别距离时代广场1800m和2400m.两人分别从家中同时出发，已知小丽和小颖的速度比是2:3，结果小丽比小颖晚4min到达剧院.

(1)、求两人的速度.

(2)、要想同时达到，小颖速度不变，小丽速度需要提高m/min.

查看试题解析
23. 观察下列式子：
$(x + 1) (x^{2} - x + 1) = x^{3} + 1$ ;

$(x + 2) (x^{2} - 2 x + 4) = x^{3} + 8$ ;

$(2 m + n) (4 m^{2} - 2 m n + n^{2}) = 8 m^{3} + n^{3}$ ;

……

(1)、上面的整式乘法计算结果比较简洁，类比学习过的平方差公式，完全平方公式的推导过程，请你写出一个新的乘法公式（用含a、b的字母表示），并加以证明；

(2)、直接用你发现的公式写出计算结果：（2a+3b）（4a²﹣6ab+9b²）=；

(3)、分解因式：m³+ n ³+ 3mn（m + n）.

查看试题解析
24. 背景知识：
如图（2），在Rt△ABC中，∠ACB=90°， $A C = B C$ ，则： $A B = \sqrt{2} A C = \sqrt{2} B C$ .

(1)、解决问题：
如图（2），∠ACD = 90°，AC = DC，MN是过点A的直线，过点D作DB⊥MN于点B，连接CB，试探究线段BA、BC、BD之间的数量关系.

不妨过点C作CE⊥CB，与MN交于点E，易发现图中出现了一对全等三角形，即≌ ，由此可得线段BA、BC、BD之间的数量关系是：.

(2)、类比探究：
将图（2）中的MN绕点A旋转到图（3）的位置，其它条件不变，试探究线段BA、BC、BD之间的数量关系，并证明.

(3)、拓展应用：
将图（2）中的MN绕点A旋转到图（4）的位置，其它条件不变，若BD=2，BC= $\sqrt{2}$ ，则AB的长为.

查看试题解析