山东省枣庄市2018-2019学年九年级下学期数学期中考试试卷
试卷更新日期：2019-12-27 类型：期中考试
一、选择题：本大题共12小题，每小题3分，共36分。
-
1. - 的倒数是（ ）A、-2019 B、- C、2019 D、2. 下列运算正确的是（ ）A、（-a2）3=-a5 B、a3·a5=a15 C、（-a2b3）2=a4b6 D、3a2-2a2=13. 如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=32°，则∠GHC等于（ ）
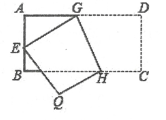A、106° B、108° C、110° D、112°4. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（ ）
A、主视图 B、左视图 C、俯视图 D、主视图和左视图5. 下列说法正确的是（ ）A、为了解我国中学生课外阅读的情况，应采取全面调查的方式 B、一组数据1、2、5、5、5、3、3的中位数和众数都是5 C、若甲组数据的方差是0.03，乙组数据的方差是0.1，则甲组数据比乙组数据稳定 D、抛掷一枚硬币100次，一定有50次“正面朝上”6. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等.交易其一，金轻十三两.问金、银一枚各重几何？”.意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等.两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（ ）A、 B、 C、 D、7. 如图，在平面直角坐标系中，直线l1：y=- x+1与x轴，y轴分别交于点A和点B，直线l1：y=kx（k≠0）与直线h在第一象限交于点C.若∠BOC=∠BCO，则k的值为（ ）
A、 B、 C、 D、28. 如图，已知一个直角三角板的直角顶点与原点重合，另两个顶点A，B的坐标分别为（-1，0），（0， ）.现将该三角板向右平移使点A与点O重合，得到△OCB，则点B的对应点B’的坐标是（ ）
A、（1，0） B、（ ， ） C、（1， ） D、（-1， ）9. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息.已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲，y米步行的速度为60米/分；②乙走完全程用了32分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有300米。其中正确的结论有（ ）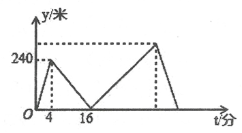
A、1个 B、2个 C、3个 D、4个10. 如图，旗杆及升旗台的剖面和教学楼的剖面在同一平面上，旗杆与地面垂直，在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°，升旗台底部到教学楼底部的距离DE=7米，升旗台坡面CD的坡度i=1：0.75，坡长CD=2米，若旗杆底部到坡面CD的水平距离BC=1米，则旗杆AB的高度约为（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.6）（ ）
A、12.6米 B、13.1米 C、14.7米 D、16.3米11. 如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（-1，0），则①二次函数的最大值为a+b+c；②a-b+c<0；③b2-4ac<0；④当y>0时，-1<x<3.其中正确的个数是（ ）
A、1 B、2 C、3 D、412. 如图，在扇形OAB中，∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，点D在OB上，点E在OB的延长线上，若正方形CDEF的边长为1，则图中阴影部分的面积为（ ）
A、 B、 -1 C、π-2 D、2π-4二、填空题：本题共6小题，每小题填对得4分，共24分.
-
13. 我省某市大力推动新旧动能转换，产业转型升级迈出新步伐.建立了新旧动能转换项目库，筛选论证项目377个，计划总投资4147亿元.4147亿元用科学记数法表示为元.14. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中，四个直角三角形都是全等的，它们的两直角边之比均为2：3.现随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为.
15. 如图，在直角△ABC中，∠C=90°，AC=6，BC=8，P、Q分别为边BC、AB上的两个动点，若要使△APQ是等腰三角形且△BPQ是直角三角形，则AQ=.
16. 三角形的两边长分别为3和6，第三边的长是方程x2-6x+8=0的解，则此三角形周长是.17. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度.
18. 如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B22边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1 ， △B2C1B3的面积为S₂ ， △B3C2B4的面积为S3 ， 如此下去，则Sn= .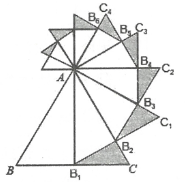
三、解答题：本题共7小题，满分60分。
-
19. 先化简，再求值：（ -1）÷ ，其中x= +1.20. 七年级（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图.
男、女生所选项目人数统计表：
项目
男生（人数）
女生（人数）
机器人
7
9
3D打印
m
4
航模
2
2
其他
5
n
学生所选项目人数扇形统计图
根据以上信息解决下列问题：
(1)、m= ， n=；(2)、扇形统计图中机器人项目所对应扇形的圆心角度数为°；(3)、从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率。21. 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．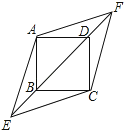
(1)、求证：△ABE≌△ADF；(2)、试判断四边形AECF的形状，并说明理由．22. 某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同。(1)、求甲、乙两种树苗每棵的价格各是多少元？(2)、在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？23. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B.AC经过圆心O并与圆相交于点D、C，过C作直线CE⊥AB，交AB的延长线于点E.
(1)、求证：CB平分∠ACE；(2)、若BE=3，CE=4，求⊙O的半径。24. 如图，已知点D在反比例函数y=2的图象上，过点D作DB⊥y轴，垂足为B（0，3），直线y=kx+b经过点A（5，0），与y轴交于点C，且BD=OC，OC：OA=2：5.
(1)、求反比例函数y= 和一次函数y=kx+b的表达式；(2)、直接写出关于x的不等式 >kx+b的解集.25. 如图，已知二次函数y=ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）。点P是直线BC上方的抛物线上一动点
(1)、求二次函数y=ax2+2x+c的表达式；(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POPC.若四边形POP'C为菱形，请求出此时点P的坐标；(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积.