山东省滨州市惠民县部分校联考2018-2019学年中考数学一模试卷
试卷更新日期:2019-12-27 类型:中考模拟
一、选择题:本大题共12个小题,每小题3分,满分36分.
-
1. 在0.3,-3,0,- 这四个数中,最大的是( )A、0.3 B、-3 C、0 D、-2. 下列运算正确的是( )A、(2a2)3=6a6 B、-x6÷x2=-x4 C、2x+2y=4xy D、(x-1)2=x2-123. 如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
 A、
A、 B、
B、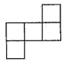 C、
C、 D、
D、 4. 2018年我国自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,其中的一个大数据中心能存储58000000000本书籍,将58000000000用科学记数法表示应为( )A、58×109 B、5.8×1010 C、5.8×1011 D、0.58×10115. 在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩(单位:个)分别为:( )
4. 2018年我国自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,其中的一个大数据中心能存储58000000000本书籍,将58000000000用科学记数法表示应为( )A、58×109 B、5.8×1010 C、5.8×1011 D、0.58×10115. 在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩(单位:个)分别为:( )24,20,19,20,22,23,20,22.则这组数据中的众数和中位数分别是
A、22个、20个 B、22个、21个 C、20个、21个 D、20个、22个6. 同一根细铁丝可以折成边长为10cm的等边三角形,也可以折成面积为50cm2的矩形.设所折成的矩形的一边长为xcm,则可列方程为( )A、x(10-x)=50 B、x(30-x)=50 C、x(15-x)=50 D、x(30-2x)=507. 如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( ) A、30° B、60° C、50° D、40°8. 如图,五一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从C,D出口离开的概率是( )
A、30° B、60° C、50° D、40°8. 如图,五一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从C,D出口离开的概率是( )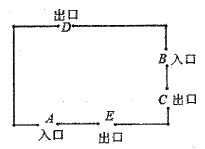 A、 B、 C、 D、9. 如图,OO是△ABC的外接圆,BC=3,∠BAC=30°,则劣弧
A、 B、 C、 D、9. 如图,OO是△ABC的外接圆,BC=3,∠BAC=30°,则劣弧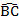 的长等于( )
的长等于( )  A、 B、π C、 D、10. 如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
A、 B、π C、 D、10. 如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( ) A、AE=BF B、∠DAE=∠BFC C、∠AEB+∠BFC=90° D、AE⊥BF11. 一座人行天桥如图所示,坡面BC的铅直高度与水平宽度的比为1:2,为了方便市民推车过天桥,有关部门决定在保持天桥高度的前提下,降低坡度,使新坡面AC的坡度为1:3,AB=6m,则天桥高度CD为( )
A、AE=BF B、∠DAE=∠BFC C、∠AEB+∠BFC=90° D、AE⊥BF11. 一座人行天桥如图所示,坡面BC的铅直高度与水平宽度的比为1:2,为了方便市民推车过天桥,有关部门决定在保持天桥高度的前提下,降低坡度,使新坡面AC的坡度为1:3,AB=6m,则天桥高度CD为( ) A、6m B、6 m C、7m D、8m12. 在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A、6m B、6 m C、7m D、8m12. 在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A、3 B、5 C、3或5 D、3或6二、填空题:本大题共8个小题,每小题5分,满分40分。
-
13. 因式分解:16x4-y4=.14. 不等式组 的整数解是.15. 某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按A,B,C,D四个等级进行评分,然后根据统计结果绘制了如图两幅不完整的统计图,那么此次抽取的作品中等级为B的作品数为.
 16. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A'B'C可以由△ABC绕点C顺时针旋转得到,其中点A'与点A是对应点,点B与点B是对应点,连接AB',且A、B’、A'在同一条直线上,则AA’的长为.
16. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A'B'C可以由△ABC绕点C顺时针旋转得到,其中点A'与点A是对应点,点B与点B是对应点,连接AB',且A、B’、A'在同一条直线上,则AA’的长为.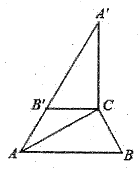 17. 如图,△ABC中,∠ACB=90°,AC=BC=4,点D,E分别是AB、AC的中点,在CD上找一点P,连接AP、EP,当AP+EP最小时,这个最小值是.
17. 如图,△ABC中,∠ACB=90°,AC=BC=4,点D,E分别是AB、AC的中点,在CD上找一点P,连接AP、EP,当AP+EP最小时,这个最小值是. 18. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,连接FB,那么tan∠FBC的值为.
18. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,连接FB,那么tan∠FBC的值为.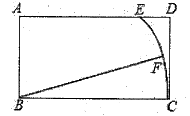 19. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数y= 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为.
19. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数y= 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为. 20. 如图是一个运算程序的示意图,若开始输入x的值为625,则第2019次输出的结果为
20. 如图是一个运算程序的示意图,若开始输入x的值为625,则第2019次输出的结果为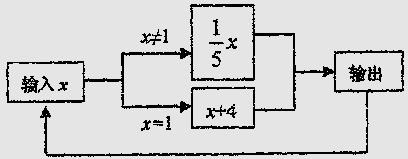
三、解答题:本大题共6个小题,满分74分.
-
21. 先化简,再求值 ,其中a=2.22. 张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米。假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示。
 (1)、求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;(2)、求图中a的值;(3)、求张师傅途中加油多少升?23. 景观大道要进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要370元;购买A种树苗5棵,B种树苗2棵,需要430元.(1)、求购买A,B两种树苗每棵各需多少元?(2)、现需购买这两种树苗共100棵,要求购买这两种树苗的资金不超过5860元,求最多能购买多少棵A种树苗?24. 如图,点D是以AB为直径的半圆O上一点,连接BD,点C是AD的中点,过点C作直线BD的垂线,垂足为点E.
(1)、求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;(2)、求图中a的值;(3)、求张师傅途中加油多少升?23. 景观大道要进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要370元;购买A种树苗5棵,B种树苗2棵,需要430元.(1)、求购买A,B两种树苗每棵各需多少元?(2)、现需购买这两种树苗共100棵,要求购买这两种树苗的资金不超过5860元,求最多能购买多少棵A种树苗?24. 如图,点D是以AB为直径的半圆O上一点,连接BD,点C是AD的中点,过点C作直线BD的垂线,垂足为点E.
求证:
(1)、CE是半圆O的切线;(2)、BC2=AB·BE.25. 定义:有一个内角为90°,且对角线相等的四边形称为准矩形.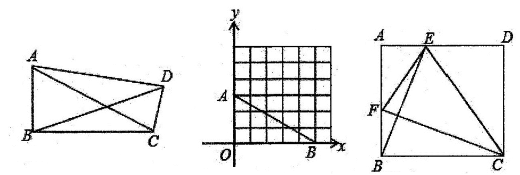
图1 图2 图3
(1)、①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=;(2)、如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CFLBE,求证:四边形BCEF是准矩形;(3)、已知准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是.26. 如图,抛物线y=x2+bx+c与x轴交于点4和点B(3,0),与y轴交于点C(0,3).
 (1)、求抛物线y=x2+bx+c的解析式;(2)、点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
(1)、求抛物线y=x2+bx+c的解析式;(2)、点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.