2017年湖南省长沙市高考数学模拟试卷（理科）（5月份）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题

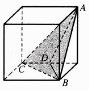
1. 已知集合P= ${x | - 2016 \leq x \leq 2017} ， Q = {x | \sqrt{2017 - x} < 1}$ ，则P∩Q=（）

A、（2016，2017） B、（2016，2017] C、[2016，2017） D、（﹣2016，2017）

查看试题解析
2. 若复数z满足 $2 z + z \cdot \bar{z} = {(2 - i)}^{2}$ （i为虚数单位），则z为（）

A、﹣1﹣2i B、﹣1﹣i C、﹣1+2i D、1﹣2i

查看试题解析
3. 已知变量x，y满足 ${\begin{matrix} 2 x - y \leq 0 \\ x - 2 y + 3 \geq 0 \\ x \geq 0 \end{matrix}$ ，则z=8^x•2^y的最大值为（）

A、33 B、32 C、35 D、34

查看试题解析
4. 如图是一个正方体，A，B，C为三个顶点，D是棱的中点，则三棱锥A﹣BCD的正视图，俯视图是（注：选项中的上图是正视图，下图是俯视图）（）

A、 B、 C、 D、

查看试题解析
5. 为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系，随机调查了该社区5户家庭，得到如下统计数据表：
购买食品的年支出费用x（万元）
2.09
2.15
2.50
2.84
2.92
购买水果和牛奶的年支出费用y（万元）
1.25
1.30
1.50
1.70
1.75
根据上表可得回归直线方程 $\hat{y} = \hat{b} x + \hat{a}$ ，其中 $\hat{b} = 0.85 ， \hat{a} = \bar{y} - \hat{b} \bar{x}$ ，据此估计，该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为（）

A、1.79万元 B、2.55万元 C、1.91万元 D、1.94万元

查看试题解析
6. 执行如图所示的程序框图，如果输入的m=15，n=12，则输出的n是（）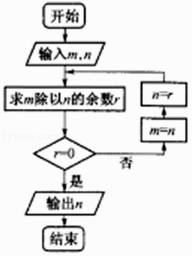

A、15 B、12 C、3 D、180

查看试题解析
7. 某班级有一个学生A在操场上绕圆形跑道逆时针方向匀速跑步，每52秒跑一圈，在学生A开始跑步时，在教室内有一个学生B往操场看了一次，以后每50秒往操场上看一次，则该学生B“感觉”到学生A的运动是（）

A、逆时针方向匀速前跑 B、顺时针方向匀速前跑 C、顺时针方向匀速后退 D、静止不动

查看试题解析
8. 已知 $| \vec{a} | = 1$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{3}$ ， $(\vec{a} + 2 \vec{b}) \cdot \vec{a} = 3$ ，则 $| \vec{b} |$ 的值是（）

A、3 B、1 C、 $\sqrt{2}$ D、2

查看试题解析
9. 随机地取两个数x，y，使得x∈[﹣1，1]，y∈[0，1]，则满足y≥x²的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
10. 已知函数f（x）= $\frac{\sqrt{3}}{2}$ sin（x+ $\frac{π}{6}$ ）﹣ $\frac{1}{2}$ cos（x+ $\frac{π}{6}$ ），若存在x₁ ， x₂ ， x₃ ， …，x_n满足0≤x₁＜x₂＜x₃＜…＜x_n≤6π，且|f（x₁）﹣f（x₂）|+|f（x₂）﹣f（x₃）|+… $+ | f (x_{n - 1}) - f (x_{n}) | = 12 (n \geq 2 ， n \in N^{*})$ ，则n的最小值为（）

A、6 B、10 C、8 D、12

查看试题解析
11. $\sum_{k = 0}^{m} C_{n - k}^{n - m} C_{n}^{k}$ =（）

A、2^m⁺ⁿ B、 $\frac{C_{n}^{m}}{2^{m}}$ C、 $2^{n} C_{n}^{m}$ D、 $2^{m} C_{n}^{m}$

查看试题解析
12. 平面α过正方体ABCD﹣A₁B₁C₁D₁的面对角线 $A B_{1}^{}$ ，且平面α⊥平面C₁BD，平面α∩平面ADD₁A₁=AS，则∠A₁AS的正切值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

13. 定义运算： $x \nabla y = {\begin{matrix} x (x y \geq 0) \\ y (x y < 0) \end{matrix}$ ，例如：3∇4=3，（﹣2）∇4=4，则函数f（x）=x²∇（2x﹣x²）的最大值为．

查看试题解析
14. 已知 $α - β = \frac{π}{3} ， t a n α - t a n β = 3$ ，则cos（α+β）的值为．

查看试题解析
15. 锐角△ABC中，D为BC的中点，满足∠BAD+∠C=90°，则角B，C的大小关系为．（填“B＜C”或“B=C”或B＞C）

查看试题解析
16. 在半径为R的圆内，作内接等腰△ABC，当底边上高h∈（0，t]时，△ABC的面积取得最大值 $\frac{3 \sqrt{3} R^{2}}{4}$ ，则t的取值范围是．

查看试题解析

三、解答题

17. 设数列{a_n}的前n项和为S_n ，若点 $A_{n} (n ， \frac{S_{n}}{n})$ 在函数f（x）=﹣x+c的图象上运动，其中c是与x无关的常数，且a₁=3．

(1)、求数列{a_n}的通项公式；

(2)、记 $b_{n} = a_{a_{n}}$ ，求数列{b_n}的前n项和T_n的最小值．

查看试题解析
18. 某班级50名学生的考试分数x分布在区间[50，100）内，设分数x的分布频率是f（x）且f（x）= ${\begin{matrix} \frac{n}{10} - 0.4 ， 10 n \leq x < 10 (n + 1) ， n = 5 ， 6 ， 7 \\ - \frac{n}{5} + b ， 10 n \leq x < 10 (n + 1) ， n = 8 ， 9 \end{matrix}$ ，考试成绩采用“5分制”，规定：考试分数在[50，60）内的成绩记为1分，考试分数在[60，70）内的成绩记为2分，考试分数在[70，80）内的成绩记为3分，考试分数在[80，90）内的成绩记为4分，考试分数在[90，100）内的成绩记为5分．用分层抽样的方法，现在从成绩在1分，2分及3分的人中用分层抽样随机抽出6人，再从这6人中抽出3人，记这3人的成绩之和为ξ（将频率视为概率）．

(1)、求b的值，并估计班级的考试平均分数；

(2)、求P（ξ=7）；

(3)、求ξ的分布列和数学期望．

查看试题解析
19. 如图，已知正方形ABCD和矩形ACEF所在平面相互垂直，AB= $\sqrt{2}$ ，AF=1，G为线段AD上的任意一点．

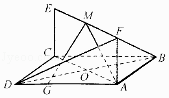(1)、若M是线段EF的中点，证明：平面AMG⊥平面BDF；

(2)、若N为线段EF上任意一点，设直线AN与平面ABF，平面BDF所成角分别是α，β，求 $\frac{s i n α}{s i n β}$ 的取值范围．

查看试题解析
20. 已知 $P (\sqrt{3} ， \frac{1}{2})$ 在椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上，F为右焦点，PF⊥垂直于x轴，A，B，C，D为椭圆上的四个动点，且AC，BD交于原点O．

(1)、求椭圆C的方程；

(2)、判断直线l： $\frac{m + n}{2} x + (m - n) y = \frac{\sqrt{3} + 1}{2} m + \frac{\sqrt{3} - 1}{2} n (m ， n \in R)$ 与椭圆的位置关系；

(3)、设A（x₁ ， y₁），B（x₂ ， y₂）满足 $\frac{y_{1} y_{2}}{\vec{O A} \cdot \vec{O B}}$ = $\frac{1}{5}$ ，判断k_AB+k_BC的值是否为定值，若是，请求出此定值，并求出四边形ABCD面积的最大值，否则说明理由．

查看试题解析
21. 已知f（x）=ax³﹣x²﹣x+b（a，b∈R，a≠0），g（x）= $\frac{3 \sqrt{e}}{4} e^{x}$ （e是自然对数的底数），f（x）的图象在x=﹣ $\frac{1}{2}$ 处的切线方程为y= $\frac{3}{4} x + \frac{9}{8}$ ．

(1)、求a，b的值；

(2)、探究直线y= $\frac{3}{4} x + \frac{9}{8}$ ．是否可以与函数g（x）的图象相切？若可以，写出切点的坐标，否则，说明理由；

(3)、证明：当x∈（﹣∞，2]时，f（x）≤g（x）．

查看试题解析
22. 平面直角坐标系xOy中，直线l的参数方程是 ${\begin{matrix} x = \sqrt{3} + t c o s \frac{π}{4} \\ y = t s i n \frac{π}{4} \end{matrix}$ （t为参数），以射线ox为极轴建立极坐标系，曲线C的极坐标方程是 $\frac{ρ^{2} c o s^{2} θ}{4}$ +ρ²sin²θ=1．

(1)、求曲线C的直角坐标方程；

(2)、求直线l与曲线C相交所得的弦AB的长．

查看试题解析
23. 已知函数f（x）= $\frac{1}{4} {(x + 1)}^{2}$ ．

(1)、证明：f（x）+|f（x）﹣2|≥2；

(2)、当x≠﹣1时，求y= $\frac{1}{4 f (x)} + {[f (x)]}^{2}$ 的最小值．

查看试题解析

购买食品的年支出费用x（万元）	2.09	2.15	2.50	2.84	2.92
购买水果和牛奶的年支出费用y（万元）	1.25	1.30	1.50	1.70	1.75