2017年河北省保定市徐水县高考数学全真模拟试卷（理科）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题

1. 设集合A={x|x＜2}，B={y|y=2^x﹣1}，则A∩B=（）

A、（﹣∞，3） B、[2，3） C、（﹣∞，2） D、（﹣1，2）

查看试题解析
2. 若 $\frac{a + i}{1 + 2 i} = t i$ （i为虚数单位，a，t∈R），则t+a等于（）

A、﹣1 B、0 C、1 D、2

查看试题解析
3. 已知圆锥曲线mx²+y²=1的一个焦点与抛物线x²=8y的焦点重合，则此圆锥曲线的离心率为（）

A、2 B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、不能确定

查看试题解析
4. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）

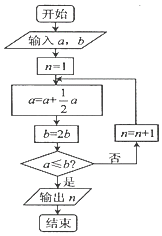A、2 B、3 C、4 D、5

查看试题解析
5. 定义在R上的函数f（x）=2^|x^﹣m|﹣1为偶函数，记a=f（log_0.53），b=f（log₂5），c=f（2m），则（）

A、a＜b＜c B、a＜c＜b C、c＜a＜b D、c＜b＜a

查看试题解析
6. 已知数列{a_n}为等差数列，S_n其前n项和，且a₂=3a₄﹣6，则S₉等于（）

A、25 B、27 C、50 D、54

查看试题解析
7. 如图是某个几何体的三视图，则该几何体的体积是（）

A、 $\sqrt{3}$ B、2 C、3 D、4

查看试题解析
8. 若对圆（x﹣1）²+（y﹣1）²=1上任意一点P（x，y），|3x﹣4y+a|+|3x﹣4y﹣9|的取值与x，y无关，则实数a的取值范围是（）

A、a≤﹣4 B、﹣4≤a≤6 C、a≤﹣4或a≥6 D、a≥6

查看试题解析
9. 函数f（x）=cos（ωx+ $\frac{π}{6}$ ）（ω＞0）在[0，π]内的值域为[﹣1， $\frac{\sqrt{3}}{2}$ ]，则ω的取值范围是（）

A、[ $\frac{3}{2}$ ， $\frac{5}{3}$ ] B、[ $\frac{5}{6}$ ， $\frac{3}{2}$ ] C、[ $\frac{5}{6}$ ，+∞） D、[ $\frac{5}{6}$ ， $\frac{5}{3}$ ]

查看试题解析
10. 抛物线C：y²=4x的焦点为F，N为准线上一点，M为y轴上一点，∠MNF为直角，若线段MF的中点E在抛物线C上，则△MNF的面积为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $3 \sqrt{2}$

查看试题解析
11. 体积为 $18 \sqrt{3}$ 的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上，球心O在此三棱锥内部，且R：BC=2：3，点E为线段BD上一点，且DE=2EB，过点E作球O的截面，则所得截面圆面积的取值范围是（）

A、[4π，12π] B、[8π，16π] C、[8π，12π] D、[12π，16π]

查看试题解析
12. 设函数f（x）满足xf′（x）+f（x）= $\frac{l n x}{x}$ ，f（e）= $\frac{1}{e}$ ，则函数f（x）（）

A、在（0，e）上单调递增，在（e，+∞）上单调递减 B、在（0，+∞）上单调递增 C、在（0，e）上单调递减，在（e，+∞）上单调递增 D、在（0，+∞）上单调递减

查看试题解析

二、填空题

13. （1+2x²）（x﹣ $\frac{1}{x}$ ）⁸的展开式中常数项为．

查看试题解析
14. 已知向量| $\vec{a}$ |=2， $\vec{b}$ 与（ $\vec{b}$ ﹣ $\vec{a}$ ）的夹角为30°，则| $\vec{b}$ |最大值为．

查看试题解析
15. 不等式组 ${\begin{matrix} y - 1 \geq 0 \\ x - y + 2 \geq 0 \\ x + 4 y - 8 \leq 0 \end{matrix}$ 表示的平面区域为Ω，直线x=a（a＞1）将Ω分成面积之比为1：4的两部分，则目标函数z=ax+y的最大值为．

查看试题解析
16. 如图，在直角坐标系xOy中，将直线y= $\frac{x}{2}$ 与直线x=1及x轴所围成的图形（阴影部分）绕x轴旋转一周得到一个圆锥，圆锥的体积V_圆锥= $\int_{0}^{1}$ π（ $\frac{x}{2}$ ）²dx= $\frac{π}{12}$ x³| $_{0}^{1}$ = $\frac{π}{12}$ ．据此类比：将曲线y=x³（x≥0）与直线y=8及y轴所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V= ．

查看试题解析

三、解答题

17. 数列{a_n}的前n项和为S_n ， S_n=（2ⁿ﹣1）a_n ，且a₁=1．

(1)、求数列{a_n}的通项公式；

(2)、若b_n=na_n ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 某校举行运动会，其中三级跳远的成绩在8.0米（四舍五入，精确到0.1米）以上的进入决赛，把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．
（Ⅰ）求进入决赛的人数；
（Ⅱ）若从该校学生（人数很多）中随机抽取两名，记X表示两人中进入决赛的人数，求X的分布列及数学期望；
（Ⅲ）经过多次测试后发现，甲成绩均匀分布在8～10米之间，乙成绩均匀分布在9.5～10.5米之间，现甲，乙各跳一次，求甲比乙远的概率．

查看试题解析
19. 如图，平行四边形ABCD中，BC=2AB=4，∠ABC=60°，PA⊥AD，E，F分别为BC，PE的中点，AF⊥平面PED．

(1)、求证：PA⊥平面ABCD；

(2)、求直线BF与平面AFD所成角的正弦值．

查看试题解析
20.
如图，椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的右顶点为A（2，0），左、右焦点分别为F₁、F₂ ，过点A且斜率为 $\frac{1}{2}$ 的直线与y轴交于点P，与椭圆交于另一个点B，且点B在x轴上的射影恰好为点F₁ ．

（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过点P且斜率大于 $\frac{1}{2}$ 的直线与椭圆交于M，N两点（|PM|＞|PN|），若S_△_PAM：S_△_PBN=λ，求实数λ的取值范围．

查看试题解析
21. 已知函数f（x）=axln（x+1）+x+1（x＞﹣1，a∈R）．

(1)、若 $a = \frac{1}{e}$ ，求函数f（x）的单调区间；

(2)、当x≥0时，不等式f（x）≤e^x恒成立，求实数a的取值范围．

查看试题解析
22. 已知曲线C₁的参数方程为 ${\begin{matrix} x = 2 t - 1 \\ y = - 4 t - 2 \end{matrix}$ （t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为 $ρ = \frac{2}{1 - c o s θ}$ ．
（I）求曲线C₂的直角坐标系方程；
（II）设M₁是曲线C₁上的点，M₂是曲线C₂上的点，求|M₁M₂|的最小值．

查看试题解析
23. 设函数f（x）=|x+ $\frac{8}{m}$ |+|x﹣2m|（m＞0）．
（Ⅰ）求证：f（x）≥8恒成立；
（Ⅱ）求使得不等式f（1）＞10成立的实数m的取值范围．

查看试题解析