2017年贵州省铜仁四中高考数学模拟试卷（理科）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题

1. 设i为虚数单位，若复数 $\frac{z}{- i}$ 在复平面内对应的点为（1，2），则z=（）

A、﹣2+i B、2﹣i C、﹣1+2i D、1﹣2i

查看试题解析
2. 已知复数m=4﹣xi，n=3+2i，若复数 $\frac{n}{m}$ ∈R，则实数x的值为（）

A、﹣6 B、6 C、 $\frac{8}{3}$ D、﹣ $\frac{8}{3}$

查看试题解析
3. 已知双曲线 $\frac{x^{2}}{a - 3}$ + $\frac{y^{2}}{2 - a}$ =1，焦点在y轴上，若焦距为4，则a等于（）

A、 $\frac{3}{2}$ B、5 C、7 D、 $\frac{1}{2}$

查看试题解析
4. 已知 $c o s (\frac{2}{3} π - 2 θ) = - \frac{7}{9}$ ，则 $s i n (\frac{π}{6} + θ)$ 的值等于（）

A、 $\frac{1}{3}$ B、 $\pm \frac{1}{3}$ C、 $- \frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
5. 某程序框图如图所示，则该程序运行后输出的值是（）

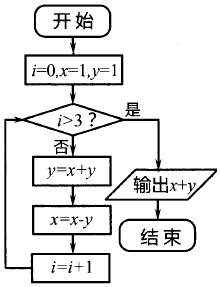A、0 B、﹣1 C、﹣2 D、﹣8

查看试题解析
6. 在平面直角坐标系中，角α的顶点与原点O重合，始边与x轴的非负半轴重合，点P（﹣2t，t）（t≠0）是角α终边上的一点，则 $t a n (α + \frac{π}{4})$ 的值为（）

A、 $3 - 2 \sqrt{2}$ B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
7. 设实数x，y满足 ${\begin{matrix} x + y - 6 \geq 0 \\ x + 2 y - 14 \leq 0 \\ 2 x + y - 10 \leq 0 \end{matrix}$ ，则2xy的最大值为（）

A、25 B、49 C、12 D、24

查看试题解析
8. 已知等比数列{a_n}，且a₆+a₈= $\int_{0}^{4} \sqrt{16 - x^{2}} d x$ ，则a₈（a₄+2a₆+a₈）的值为（）

A、π² B、4π² C、8π² D、16π²

查看试题解析
9. 某几何体的三视图如图所示，则该几何体的体积为（）

A、16π﹣ $\frac{16}{3}$ B、16π﹣ $\frac{32}{3}$ C、8π﹣ $\frac{16}{3}$ D、8π﹣ $\frac{32}{3}$

查看试题解析
10. 椭圆 $\frac{x^{2}}{5}$ + $\frac{y^{2}}{4}$ =1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{6 \sqrt{5}}{5}$ C、 $\frac{8 \sqrt{5}}{5}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
11. 四面体A﹣BCD中，AB=CD=10，AC=BD=2 $\sqrt{34}$ ，AD=BC=2 $\sqrt{41}$ ，则四面体A﹣BCD外接球的表面积为（）

A、50π B、100π C、200π D、300π

查看试题解析
12. 已知函数f（x）=x² ， g（x）=﹣1nx，g'（x）为g（x）的导函数．若存在直线l同为函数f（x）与g'（x）的切线，则直线l的斜率为（）

A、 $2 \sqrt{5} - 4$ B、2 C、4 D、 $\frac{1}{2}$

查看试题解析

二、填空题

13. 定积分 $\int_{0}^{1} (x^{2} + e^{x} - \frac{1}{3}) d x$ 的值为．

查看试题解析
14. 若数列{a_n}的前n项和为S_n ，且3S_n﹣2a_n=1，则{a_n}的通项公式是a_n= ．

查看试题解析
15. 已知双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1的右焦点为F，过点F向双曲线的一条渐进线引垂线，垂足为M，交另一条渐近线于N，若2 $\vec{M F}$ = $\vec{F N}$ ，则双曲线的离心率．

查看试题解析
16. 在△ABC中，∠A= $\frac{π}{3}$ ，O为平面内一点．且| $\vec{O A} | = | \vec{O B} | = | \vec{O C}$ |，M为劣弧 $\hat{B C}$ 上一动点，且 $\vec{O M} = p \vec{O B} + q \vec{O C}$ ．则p+q的取值范围为．

查看试题解析

三、解答题

17. 在△ABC中，角A、B、C所对的边分别是a、b、c，已知sinB+sinC=msinA（m∈R），且a²﹣4bc=0．

(1)、当a=2， $m = \frac{5}{4}$ 时，求b、c的值；

(2)、若角A为锐角，求m的取值范围．

查看试题解析
18. 医学上某种还没有完全攻克的疾病，治疗时需要通过药物控制其中的两项指标H和V．现有..三种不同配方的药剂，根据分析，A，B，C三种药剂能控制H指标的概率分别为0.5，0.6，0.75，能控制V指标的概率分别是0.6，0.5，0.4，能否控制H指标与能否控制V指标之间相互没有影响．
（Ⅰ）求A，B，C三种药剂中恰有一种能控制H指标的概率；
（Ⅱ）某种药剂能使两项指标H和V都得到控制就说该药剂有治疗效果．求三种药剂中有治疗效果的药剂种数X的分布列．

查看试题解析
19. 如图，棱柱ABCD﹣A₁B₁C₁D₁中，底面ABCD是平行四边形，侧棱AA₁⊥底面ABCD，AB=1，AC= $\sqrt{3}$ ，BC=BB₁=2．
（Ⅰ）求证：AC⊥平面ABB₁A₁；
（Ⅱ）求二面角A﹣C₁D﹣C的平面角的余弦值．

查看试题解析
20. 已知圆C₁：x²+y²=r²（r＞0）与直线l₀：y= $\frac{1}{2} x + \frac{3}{2} \sqrt{5}$ 相切，点A为圆C₁上一动点，AN⊥x轴于点N，且动点M满足 $\vec{O M} + 2 \vec{A M} = (2 \sqrt{2} - 2) \vec{O N}$ ，设动点M的轨迹为曲线C．

(1)、求动点M的轨迹曲线C的方程；

(2)、若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O，求线段PQ长度的取值范围．

查看试题解析
21. 已知函数f（x）=（x+a）ln（x+a），g（x）=﹣ $\frac{a}{2} x^{2}$ +ax．

(1)、函数h（x）=f（e^x﹣a）+g'（e^x），x∈[﹣1，1]，求函数h（x）的最小值；

(2)、对任意x∈[2，+∞），都有f（x﹣a﹣1）﹣g（x）≤0成立，求a的范围．

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{matrix} x = 4 t^{2} \\ y = 4 t \end{matrix}$ （t为参数），以O为极点x轴的正半轴为极轴建极坐标系，直线l的极坐标方程为ρ（cosθ﹣sinθ）=4，且与曲线C相交于A，B两点．
（Ⅰ）在直角坐标系下求曲线C与直线l的普通方程；
（Ⅱ）求△AOB的面积．

查看试题解析
23. 已知函数f（x）=m﹣|x﹣1|，（m＞0），且f（x+1）≥0的解集为[﹣3，3]．
（Ⅰ）求m的值；
（Ⅱ）若正实数a，b，c满足 $\frac{1}{a} + \frac{1}{2 b} + \frac{1}{3 c} = m$ ，求证：a+2b+3c≥3．

查看试题解析