2017年广西白色市高考数学模拟试卷（理科）（5月份）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题

1. 若集合A={x|y= $x^{\frac{1}{2}}$ }，B={x|y=ln（x+1）}，则A∩B=（）

A、[0，+∞） B、（0，1） C、（﹣1，+∞） D、（﹣∞，﹣1）

查看试题解析
2. 下面是关于复数z=2﹣i的四个命题：p₁：|z|=5；p₂：z²=3﹣4i；p₃：z的共轭复数为﹣2+i；p₄：z的虚部为﹣1，其中真命题为（）

A、p₂ ， p₃ B、p₁ ， p₂ C、p₂ ， p₄ D、p₃ ， p₄

查看试题解析
3. 在如图所示的矩形ABCD中，AB=4，AD=2，E为线段BC上的点，则 $\vec{A E} \cdot \vec{D E}$ 的最小值为（）

A、12 B、15 C、17 D、16

查看试题解析
4. 如图是2017年第一季度五省GDP情况图，则下列陈述正确的是（）
①2017年第一季度GDP总量和增速均居同一位的省只有1个；
②与去年同期相比，2017年第一季度五个省的GDP总量均实现了增长；
③去年同期的GDP总量前三位是江苏、山东、浙江；
④2016年同期浙江的GDP总量也是第三位．

A、①② B、②③④ C、②④ D、①③④

查看试题解析
5. 若函数f（x）=2sinωx（0＜ω＜1）在区间 $[0 ， \frac{π}{3}]$ 上的最大值为1，则ω=（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 若 $a = l o g_{\frac{1}{π}} \frac{1}{3}$ ， $b = e^{\frac{π}{3}}$ ， $c = l o g_{3} c o s \frac{1}{5} π$ ，则（）

A、b＞c＞a B、b＞a＞c C、a＞b＞c D、c＞a＞b

查看试题解析
7. 某程序框图如图所示，则该程序运行后输出的B=（）

A、15 B、29 C、31 D、63

查看试题解析
8. 在△ABC中，角A、B、C所对的边分别为a，b，c，已知a=1，b= $\sqrt{3}$ ，A=30°，B为锐角，那么角A：B：C的比值为（）

A、1：1：3 B、1：2：3 C、1：3：2 D、1：4：1

查看试题解析
9. 某几何体的三视图如图所示，则该几何体的表面积是（）

A、 $20 + 4 \sqrt{5}$ B、 $12 + 4 \sqrt{5}$ C、 $20 + 2 \sqrt{5}$ D、 $12 + 2 \sqrt{5}$

查看试题解析
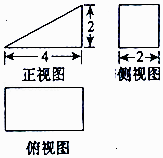10. 如图，在三棱锥A﹣BCD中，平面ABC⊥平面BCD，△BAC与△BCD均为等腰直角三角形，且∠BAC=∠BCD=90°，BC=2，点P是线段AB上的动点，若线段CD上存在点Q，使得异面直线PQ与AC成30°的角，则线段PA长的取值范围是（）

A、（0， $\frac{\sqrt{2}}{2}$ ） B、（0， $\frac{\sqrt{6}}{3}$ ） C、（ $\frac{\sqrt{2}}{2}$ ， $\sqrt{2}$ ） D、（ $\frac{\sqrt{6}}{3}$ ， $\sqrt{2}$ ）

查看试题解析
11. 设P为双曲线 $x^{2} - \frac{y^{2}}{15} = 1$ 右支上一点，M，N分别是圆（x+4）²+y²=4和（x﹣4）²+y²=1上的点，设|PM|﹣|PN|的最大值和最小值分别为m，n，则|m﹣n|=（）

A、4 B、5 C、6 D、7

查看试题解析
12. $\vec{a b}$ 表示一个两位数，十位数和个位数分别用a，b表示，记f（ $\vec{a b}$ ）=a+b+3ab，如f（ $\vec{12}$ ）=1+2+3×1×2=9，则满足f（ $\vec{a b}$ ）= $\vec{a b}$ 的两位数的个数为（）

A、15 B、13 C、9 D、7

查看试题解析

二、填空题

13. 已知实数x，y满足不等式组 ${\begin{matrix} 1 \leq x + y \leq 2 \\ - 1 \leq x - y \leq 1 \end{matrix}$ ，则z= $\frac{y + 1}{x + 1}$ 的最大值是．

查看试题解析
14. 已知 $s i n θ + c o s θ = \frac{1}{5}$ ， $θ \in (\frac{π}{2} ， π)$ ，则tanθ= ．

查看试题解析
15. 直线x=a分别与曲线y=2x+1，y=x+lnx交于A，B，则|AB|的最小值为．

查看试题解析
16. 设圆C满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3：1；③圆心到直线l：x﹣2y=0的距离为d．当d最小时，圆C的面积为．

查看试题解析

三、解答题

17. 已知各项均为正数的等差数列{a_n}满足：a₄=2a₂ ，且a₁ ， 4，a₄成等比数列，设{a_n}的前n项和为S_n ．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设数列 ${\frac{S_{n}}{n \cdot 2^{n}}}$ 的前n项和为T_n ，求证：T_n＜3．

查看试题解析
18. 某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第x年与年销量y（单位：万件）之间的关系如表：
x
1
2
3
4
y
12
28
42
56
（Ⅰ）在图中画出表中数据的散点图；
（Ⅱ）根据（Ⅰ）中的散点图拟合y与x的回归模型，并用相关系数加以说明；
（Ⅲ）建立y关于x的回归方程，预测第5年的销售量约为多少？．
附注：参考数据： $\sqrt{\sum_{i = 1}^{4} {(y_{i} - \bar{y})}^{2}} \approx 32.6$ ， $\sqrt{5} \approx 2.24$ ， $\sum_{i = 1}^{4} x_{i} y_{i} = 418$ ．
参考公式：相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ，
回归方程 $\hat{y} = \hat{a} + \hat{b} x$ 中斜率和截距的最小二乘法估计公式分别为： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

查看试题解析
19. 如图，在正三棱柱ABC﹣A₁B₁C₁中，点E，F分别是棱CC₁ ， BB₁上的点，且EC=2FB．
（Ⅰ）证明：平面AEF⊥平面ACC₁A₁；
（Ⅱ）若AB=EC=2，求二面角C﹣AF﹣E的余弦值．

查看试题解析
20. 已知椭圆C的中心在原点，焦点在x轴上，离心率 $e < \frac{\sqrt{2}}{2}$ ．以两个焦点和短轴的两个端点为顶点的四边形的周长为8，面积为 $2 \sqrt{3}$ ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若点P（x₀ ， y₀）为椭圆C上一点，直线l的方程为3x₀x+4y₀y﹣12=0，求证：直线l与椭圆C有且只有一个交点．

查看试题解析
21. 设函数 $f (x) = m l n x + \frac{n}{x}$ ，曲线y=f（x）在点（1，f（1））处的切线方程为y=x﹣1．
（Ⅰ）求实数m，n的值；
（Ⅱ）若b＞a＞1， $A = f (\frac{a + b}{2})$ ， $B = \frac{f (a) + f (b)}{2}$ ， $C = \frac{b f (b) - a f (a)}{b - a} - 1$ ，试判断A，B，C三者是否有确定的大小关系，并说明理由．

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{matrix} x = 3 c o s α \\ y = \sqrt{3} s i n α \end{matrix}$ （α为参数）．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为 $ρ c o s (θ + \frac{π}{3}) = \sqrt{3}$ ．
（Ⅰ）求直线l的直角坐标方程和曲线C的普通方程；
（Ⅱ）设点P为曲线C上任意一点，求点P到直线l的距离的最大值．

查看试题解析
23. 已知函数 $f (x) = | x - a | + \frac{1}{2 a} (a \neq 0)$

(1)、若不等式f（x）﹣f（x+m）≤1恒成立，求实数m的最大值；

(2)、当a＜ $\frac{1}{2}$ 时，函数g（x）=f（x）+|2x﹣1|有零点，求实数a的取值范围．

查看试题解析