河南省驻马店市确山县2019-2020学年七年级上学期期中数学试题

试卷更新日期：2019-12-27 类型：期中考试

进入出卷网下载

一、单选题

1. 在下面的四个有理数中，最小的是（）

A、﹣1 B、0 C、1 D、﹣2

查看试题解析
2. 下列各组数中，互为相反数的是（）

A、﹣1与（﹣1）² B、（﹣1）²与1 C、2与 $\frac{1}{2}$ D、2与|﹣2|

查看试题解析
3. 习近平同志在十九大报告中指出：农业农村农民问题是关系到国计民生的根本性问题，我国现有农村人口约为589 730 000人，将589 730 000用科学记数法表示为（）

A、589 73×10⁴ B、589.73×10⁶ C、5.8973×10⁸ D、0.58973×10⁸

查看试题解析
4. 下列各式计算正确的是（　　）

A、6a+a＝7a² B、﹣2a+5b＝3ab C、4m²n﹣2mn²＝2mn D、3ab²﹣5b²a＝﹣2ab²

查看试题解析
5. 在有理数2，3，﹣4，﹣5，6中，任取两个数相乘，所得积的最大值是（　　）

A、24 B、20 C、18 D、30

查看试题解析
6. 已知﹣2m⁶n与5m^2xn^y的和是单项式，则（　　）

A、x＝2，y＝1 B、x＝3，y＝1 C、x＝ $\frac{3}{2}$ ，y＝1 D、x＝1，y＝3

查看试题解析
7. 下列语句：①一个数的绝对值一定是正数； ②-a一定是一个负数；③没有绝对值为-3的数；④若|a|=a，则a是一个正数；⑤离原点左边越远的数就越小；正确的有（）个.

A、0 B、3 C、2 D、4

查看试题解析
8. 下列结论中正确的是（）

A、单项式 $\frac{π x y^{2}}{7}$ 的系数是 $\frac{1}{7}$ ，次数是4 B、单项式m的次数是1，没有系数 C、单项式﹣xy²z的系数是﹣1，次数是4 D、多项式2x²+xy²+3是二次三项式

查看试题解析
9. 下列说法正确的是（　　）

A、近似数2.0精确到了个位 B、近似数2.1与近似数2.10的精确度一样 C、用四舍五入法对3.355取近似值，精确到百分位为3.35 D、近似数5.2万精确到了千位

查看试题解析
10. 已知代数式x+2y的值是3．则代数式2x+4y﹣8的值是（　　）

A、-2 B、2 C、﹣14 D、不能确定

查看试题解析
11. 整式x²+ax﹣2y+7﹣(bx²﹣2x+9y﹣1)的值与x的取值无关，则a+b的值为

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
12. 计算：3¹+1＝4，3²+1＝10，3³+1＝28，3⁴+1＝82，3⁵+1＝244，…，归纳计算结果中的个位数字的规律，猜测3²⁰¹¹+1的个位数字是（　　）

A、0 B、2 C、4 D、8

查看试题解析

二、填空题

13. 如果向北走10m记作+10m ，那么向南走15m记作m ．

查看试题解析
14. 绝对值等于它本身的数是和．

查看试题解析
15. 如果 $| a + 2 | + {(b - 3)}^{2} = 0$ ，那么 $a^{b}$ =.

查看试题解析
16. 计算﹣3³÷（﹣3）×[﹣（﹣2）³]的结果为．

查看试题解析
17. 数轴上表示点A的数是最大的负整数，则与点A相距3个单位长度的点表示的数是．

查看试题解析
18. 请写出一个只含字母x的整式，满足当x＝2时，它的值等于﹣3．你写的整式是．

查看试题解析
19. 在如图所的运算流程中，若输入的数x=-7，则输出的数y=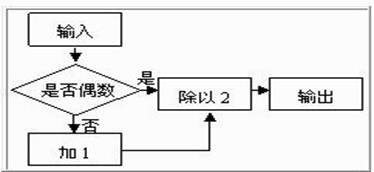

查看试题解析
20. 我们用[a]表示不大于a的最大整数，例如：[1.5]=1，[﹣2.3]=﹣3，则[﹣5.2]+[﹣0.3]+[2.2]=

查看试题解析
21. 按图中规矩摆放三角形，按照摆放规律．第（n）个图形中三角形的个数为（用含n的代数式表示）

查看试题解析

三、解答题

22. 计算：

(1)、（﹣7）×（﹣5）﹣90÷（﹣15）

(2)、（﹣1）³﹣（1﹣ $\frac{1}{2}$ ）÷3×[（﹣2）²﹣5]

(3)、（﹣1 $\frac{1}{2}$ ）²× $\frac{2}{3}$ ÷|﹣3|+（﹣0.25）÷（ $\frac{1}{2}$ ）⁶

(4)、﹣3²﹣12×（﹣ $\frac{1}{4} - \frac{2}{3} + 1$ ）+4÷（ $\frac{1}{3} - \frac{1}{5}$ ）

查看试题解析
23. 先化简，再求值：5ab²﹣[3ab﹣2（﹣2ab²+ab）]，其中a是最小的正整数，b是绝对值最小的负整数．

查看试题解析
24. 有个填写运算符号的游戏：在“ $1 □ 2 □ 6 □ 9$ ”中的每个□内，填入 $+ ， ﹣ ， \times ， \div$ 中的某一个（可重复使用），然后计算结果．

(1)、计算： $1 + 2 ﹣ 6 ﹣ 9$ ；

(2)、若请推算 $1 \div 2 \times 6 □ 9 ＝ ﹣ 6 ，$ □内的符号；

(3)、在“ $1 □ 2 □ 6 ﹣ 9$ ”的□内填入符号后，使计算所得数最小，直接写出这个最小数．

查看试题解析
25. 已知A＝x－2y，B＝－x－4y＋1.

(1)、求2(A＋B)－(A－B)；（结果用含x，y的代数式表示）

(2)、当 $| x + 2 |$ 与 ${(y - \frac{1}{2})}^{2}$ 互为相反数时，求(1)中代数式的值．

查看试题解析
26. 某学校准备印刷一批证书，现有两个印刷厂可供选择：
甲厂收费方式：收制版费1000元，每本印刷费0.5元；

乙厂收费方式：不超过2000本时，每本收印刷费1.5元；超过2000本超过部分每本收印刷费0.25元，若该校印制证书x本．

(1)、若x 不超过2000时，甲厂的收费为元，乙厂的收费为元；

(2)、若x 超过2000时，甲厂的收费为元，乙厂的收费为元

(3)、当印制证书8000本时应该选择哪个印刷厂更节省费用？节省了多少？

(4)、请问印刷多少本证书时，甲乙两厂收费相同？

查看试题解析
27. 如图，将连续的奇数1，3，5，7……排成如下的数表，用十字形框框出5个数．

(1)、探究规律一：设十字框中间的奇数为x ，则框中五个奇数的和用含x的整式表示为，这说明被十字框框中的五个奇数的和一定是正整数n（n＞1）的倍数，这个正整数n是；

(2)、探究规律二：落在十字框中间且位于第二列的一组奇数是21，39，57，75，…，则这一组数可以用整式表示为18m+3（m为序数），同样，落在十字框中间且位于第三列的一组奇数可以表示为；（用含m的式子表示）

(3)、运用规律一：已知被十字框框中的五个奇数的和为2025，则十字框中间的奇数是，这个奇数落在从左往右第列；

(4)、运用规律二：被十字框框中的五个奇数的和可能是2020吗？若能，请求出这五个数：；若不能，请说明理由.

查看试题解析