河北省张家口市2019-2020学年高一上学期数学10月月考试卷
试卷更新日期:2019-12-27 类型:月考试卷
一、单选题
-
1. 有下列说法:
(1)0与 表示同一个集合;(2)由1,2,3组成的集合可表示为 或 ;(3)方程 的所有解的集合可表示为 ;(4)集合 是有限集.其中正确的说法是( )
A、只有(1)和(4) B、只有(2)和(3) C、只有(2) D、以上四种说法都不对2. 设集合 ,则下列关系中正确的是( )A、 B、 C、 D、3. 设 , ,能表示集合 到集合 的函数关系的是( )A、 B、
B、 C、
C、 D、
D、 4. 函数 的定义域为( )A、 B、 C、 D、5. 已知全集 ,集合 , ,则 ( )A、 B、 C、 D、6. 已知集合 , ,则 ( )A、 B、 C、 D、7. 下列各组函数中,表示同一函数的是( )A、 与 B、 与 C、 与 D、 , 与 ,8. 函数 的图象是( )A、
4. 函数 的定义域为( )A、 B、 C、 D、5. 已知全集 ,集合 , ,则 ( )A、 B、 C、 D、6. 已知集合 , ,则 ( )A、 B、 C、 D、7. 下列各组函数中,表示同一函数的是( )A、 与 B、 与 C、 与 D、 , 与 ,8. 函数 的图象是( )A、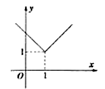 B、
B、 C、
C、 D、
D、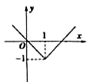 9. 方程组 的解集不可以表示为( )A、 B、 C、 D、10. 函数 、 由下列表格给出,则 ( )
9. 方程组 的解集不可以表示为( )A、 B、 C、 D、10. 函数 、 由下列表格给出,则 ( )1
2
3
4
2
4
3
1
4
3
2
1
A、4 B、3 C、2 D、1二、填空题
-
11. 若 .12. 满足 条件的集合 的个数有个.13. 设 ,则 .14. 已知函数 ,则 .15. 已知函数 为偶函数,函数 为奇函数, ,则 .16. 已知 是定义在 上的减函数,且 ,则 的范围是.17. 设全集为 ,集合 , ,则 ; .
三、解答题