2017年山东省临沂市高考数学二模试卷(理科)
试卷更新日期:2017-07-30 类型:高考模拟
一、选择题
-
1. 全集为实数集R,集合M={x||x|≤3},集合N={x|x<2},则(∁RM)∩N=( )A、{x|x<﹣3} B、{x|﹣3<x<2} C、{x|x<2} D、{x|﹣3≤x<2}2. 若 是z的共轭复数,且满足 =3+i,则z=( )A、1+2i B、﹣1+2i C、1﹣2i D、﹣1﹣2i3. 某地市高三理科学生有30000名,在一次调研测试中,数学成绩ξ~N(100,σ2),已知P(80<ξ≤100)=0.45,若按分层抽样的方式取200份试卷进行成绩分析,则应从120分以上的试卷中抽取( )A、5份 B、10份 C、15份 D、20份4. “|x﹣1|+|x+2|≤5”是“﹣3≤x≤2”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 某几何体的三视图如图所示,俯视图是半径为2的圆,则该几何体的表面积为( )
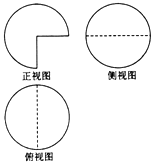 A、24π B、16π C、12π D、8π6. 将函数 的图象向右平移 个单位,再把所有点的横坐标缩短到原来的 倍(纵坐标不变),得函数y=g(x)的图象,则g(x)图象的一个对称中心为( )A、 B、 C、 D、7. 已知x,y满足 若目标函数z=﹣2x+y的最大值不超过2,则实数m的取值范围是( )A、(﹣2,2) B、[0,2] C、[﹣2,0] D、[﹣2,2]8. 在平面直角坐标系中,已知点A,B分别为x轴、y轴上的点,且|AB|=1,若点P(1, ),则 |的取值范围是( )A、[5,6] B、[5,7] C、[4,6] D、[6,9]9. 已知双曲线 与双曲线 的离心率相同,双曲线C1的左、右焦点分别为F1 , F2 , M是双曲线C1的一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 ,则双曲线C1的实轴长是( )A、32 B、16 C、8 D、410. 已知f(x)=|xex|,又g(x)=[f(x)]2﹣tf(x)(t∈R),若方程g(x)=﹣2有4个不同的根,则t的取值范围为( )A、 B、 C、 D、
A、24π B、16π C、12π D、8π6. 将函数 的图象向右平移 个单位,再把所有点的横坐标缩短到原来的 倍(纵坐标不变),得函数y=g(x)的图象,则g(x)图象的一个对称中心为( )A、 B、 C、 D、7. 已知x,y满足 若目标函数z=﹣2x+y的最大值不超过2,则实数m的取值范围是( )A、(﹣2,2) B、[0,2] C、[﹣2,0] D、[﹣2,2]8. 在平面直角坐标系中,已知点A,B分别为x轴、y轴上的点,且|AB|=1,若点P(1, ),则 |的取值范围是( )A、[5,6] B、[5,7] C、[4,6] D、[6,9]9. 已知双曲线 与双曲线 的离心率相同,双曲线C1的左、右焦点分别为F1 , F2 , M是双曲线C1的一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 ,则双曲线C1的实轴长是( )A、32 B、16 C、8 D、410. 已知f(x)=|xex|,又g(x)=[f(x)]2﹣tf(x)(t∈R),若方程g(x)=﹣2有4个不同的根,则t的取值范围为( )A、 B、 C、 D、二、填空题
-
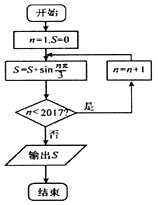
11. 已知圆x2+y2﹣2x﹣8y+1=0的圆心到直线ax﹣y+1=0的距离为1,则a= .12. 设 ,则二项式 展开式中x2项的系数为 (用数字作答).13. 阅读如图的程序框图,若运行此程序,则输出S的值为 .
 14. 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为 ,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为 .
14. 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为 ,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为 .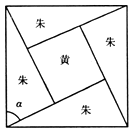 15. 定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0而是它的一个均值点.
15. 定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0而是它的一个均值点.例如y=|x|是[﹣2,2]上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数f(x)=sinx﹣1是[﹣π,π]上的“平均值函数”;
②若y=f(x)是[a,b]上的“平均值函数”,则它的均值点x0≤ ;
③若函数f(x)=x2+mx﹣1是[﹣1,1]上的“平均值函数”,则实数m∈(﹣2,0);
④若f(x)=lnx是区间[a,b](b>a≥1)上的“平均值函数”,x0是它的一个均值点,则lnx0< .
其中的真命题有(写出所有真命题的序号).
三、解答题
-
16. 已知向量 ,若f(x)=m•n.
(I)求f(x)的单调递增区间;
(II)已知△ABC的三内角A,B,C对边分别为a,b,c,且a=3,f ,sinC=2sinB,求A,c,b的值.
17. 某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:组别
文科
理科
性别
男生
女生
男生
女生
人数
3
1
3
2
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
18. 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.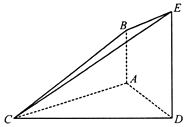
(I)求证:平面BCE⊥平面CDE;
(II)求平面BCE与平面ADEB所成锐二面角的余弦值.
19. 已知数列{an}的奇数项成等差数列,偶数项成等比数列,且公差和公比都是2,若对满足m+n≤5的任意正整数m,n,均有am+an=am+n成立.(I)求数列{an}的通项公式;
(II)若bn= ,求数列{bn}的前n项和Tn .
20. 已知函数f(x)= .(I)求函数f(x)的单调区间;
(II)若不等式f(x)> 恒成立,求整数k的最大值;
(III)求证:(1+1×2)•(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).
21. 如图,在平面直角坐标系xOy中,椭圆C1: 的离心率为 ,抛物线C2:x2=4y的焦点F是C1的一个顶点.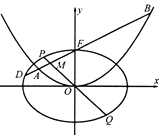
(I)求椭圆C1的方程;
(II)过点F且斜率为k的直线l交椭圆C1于另一点D,交抛物线C2于A,B两点,线段DF的中点为M,直线OM交椭圆C1于P,Q两点,记直线OM的斜率为k'.
(i)求证:k•k'=﹣ ;
(ii)△PDF的面积为S1 , △QAB的面积为是S2 , 若S1•S2=λk2 , 求实数λ的最大值及取得最大值时直线l的方程.