2017年广东省汕头市潮南区高考考前冲刺数学试卷（理科）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题

1. 若复数 $z = \frac{1 + i}{1 - i}$ ，则 $\bar{z}$ 的虚部为（）

A、1 B、﹣1 C、i D、﹣i

查看试题解析
2. 已知全集U=R，若集合M={x|﹣3＜x＜3}，N={x|2^x⁺¹﹣1≥0}，则（∁_UM）∩N=（）

A、[3，+∞） B、（﹣1，3） C、[﹣1，3） D、（3，+∞）

查看试题解析
3. 已知函数f（x）=lnx﹣（ $\frac{1}{2}$ ）^x^﹣²的零点为x₀ ，则x₀所在的区间是（）

A、（0，1） B、（1，2） C、（2，3） D、（3，4）

查看试题解析
4. 设a= $\int_{0}^{2}$ xdx，则二项式（ax﹣ $\frac{1}{\sqrt{x}}$ ）⁵展开式中含x²项的系数是（）

A、80 B、640 C、﹣160 D、﹣40

查看试题解析
5.
若执行如图的程序框图，输出S的值为4，则判断框中应填入的条件是（）

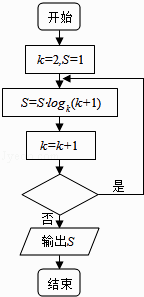A、k＜14？ B、k＜15？ C、k＜16？ D、k＜17？

查看试题解析
6. 已知实数x、y满足不等式组 ${\begin{matrix} x - 3 y + 1 \leq 0 \\ x + y - 3 \geq 0 \\ x \geq 0 \end{matrix}$ ，则x²+y²的最小值是（）

A、 $\frac{3 \sqrt{2}}{2}$ B、 $\frac{9}{2}$ C、5 D、9

查看试题解析
7. 给出下列两个命题：命题p₁：∃a，b∈（0，+∞），当a+b=1时， $\frac{1}{a}$ + $\frac{1}{b}$ =4；命题p₂：函数y=ln $\frac{1 - x}{1 + x}$ 是偶函数．则下列命题是真命题的是（）

A、p₁∧p₂ B、p₁∧（￢p₂） C、（￢p₁）∨p₂ D、（￢p₁）∨（￢p₂）

查看试题解析
8. 某几何体的三视图如图所示，则该几何体的体积是（）

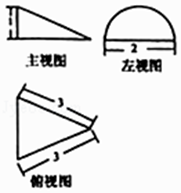A、 $\frac{\sqrt{2}}{3} π$ B、 $\frac{π}{2}$ C、 $\frac{2 \sqrt{2}}{3} π$ D、π

查看试题解析
9. 在△ABC中，3sinA+4cosB=6，4sinB+3cosA=1，则C等于（）

A、30° B、150° C、30°或150° D、60°或120°

查看试题解析
10. 已知 $\vec{a}$ 、 $\vec{b}$ 为平面向量，若 $\vec{a}$ + $\vec{b}$ 与 $\vec{a}$ 的夹角为 $\frac{π}{3}$ ， $\vec{a}$ + $\vec{b}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{4}$ ，则 $\frac{| \vec{a} |}{| \vec{b} |}$ =（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{6}}{4}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
11. 知双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0），A₁、A₂是实轴顶点，F是右焦点，B（0，b）是虚轴端点，若在线段BF上（不含端点）存在不同的两点P_i=（1，2），使得△P_iA₁A₂（i=1，2）构成以A₁A₂为斜边的直角三角形，则双曲线离心率e的取值范围是（）

A、（ $\sqrt{2}$ ， $\frac{\sqrt{6} + 1}{2}$ ） B、（ $\sqrt{2}$ ， $\frac{\sqrt{5} + 1}{2}$ ） C、（1， $\frac{\sqrt{6} + 1}{2}$ ） D、（ $\frac{\sqrt{5} + 1}{2}$ ，+∞）

查看试题解析
12. 已知等差数列{a_n}中，a₃=9，a₅=17，记数列 ${\frac{1}{a_{n}}}$ 的前n项和为S_n ，若 $S_{2 n + 1} - S_{n} \leq \frac{m}{10} ， (m \in Z)$ ，对任意的n∈N^*成立，则整数m的最小值为（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 设 $f (x) = {\begin{matrix} 1 - c o s \frac{π x}{2} ， x \in [0 ， 1] \\ \frac{1}{x} ， x \in (1 ， e] \end{matrix}$ （其中e为自然对数的底数），则y=f（x）的图象与直线y=0，x=e所围成图形的面积为．

查看试题解析
14. 已知{a_n}是等差数列，若2a₇﹣a₅=3，则a₉的值是．

查看试题解析
15. 四面体的顶点和各棱中点共10个点，则由这10点构成的直线中，有对异面直线．

查看试题解析
16. 已知函数f（x）= ${\begin{matrix} a x^{2} + 2 x + 1 ， (- 2 < x \leq 0) \\ a x - 3 ， (x > 0) \end{matrix}$ 有3个零点，则实数a的取值范围是．

查看试题解析

三、解答题

17. 已知△ABC和△A₁B₁C₁满足sinA=cosA₁ ， sinB=cosB₁ ， sinC=cosC₁ ．

(1)、求证：△ABC是钝角三角形，并求最大角的度数；

(2)、求sin²A+sin²B+sin²C的最小值．

查看试题解析
18. 为普及高中生安全逃生知识与安全防护能力，某学校高一年级举办了高中生安全知识与安全逃生能力竞赛．该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛．先将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
分数（分数段）
频数（人数）
频率
[60，70）
9
x
[70，80）
y
0.38
[80，90）
16
0.32
[90，100）
z
s
合计
p
1
（Ⅰ）求出上表中的x，y，z，s，p的值；
（Ⅱ）按规定，预赛成绩不低于90分的选手参加决赛，参加决赛的选手按照抽签方式决定出场顺序．已知高一•二班有甲、乙两名同学取得决赛资格．
①求决赛出场的顺序中，甲不在第一位、乙不在最后一位的概率；
②记高一•二班在决赛中进入前三名的人数为X，求X的分布列和数学期望．

查看试题解析
19. 已知矩形ABCD与直角梯形ABEF，∠DAF=∠FAB=90°，点G为DF的中点，AF=EF= $\frac{1}{2} A B = \sqrt{3}$ ，P在线段CD上运动．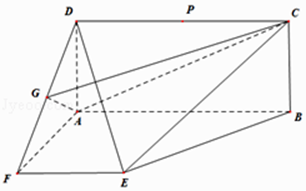

(1)、证明：BF∥平面GAC；

(2)、当P运动到CD的中点位置时，PG与PB长度之和最小，求二面角P﹣CE﹣B的余弦值．

查看试题解析
20. 已知M（ $\frac{9}{2}$ ，0），N（2，0），曲线C上的任意一点P满足： $\vec{M N}$ • $\vec{M P}$ = $\frac{15}{4}$ | $\vec{P N}$ |．
（Ⅰ）求曲线C的方程；
（Ⅱ）设曲线C与x轴的交点分别为A、B，过N的任意直线（直线与x轴不重合）与曲线C交于R、Q两点，直线AR与BQ交于点S．问：点S是否在同一直线上？若是，请求出这条直线的方程；若不是，请说明理由．

查看试题解析
21. 设函数f（x）=x²+aln（x+1）（a为常数）
（Ⅰ）若函数y=f（x）在区间[1，+∞）上是单调递增函数，求实数a的取值范围；
（Ⅱ）若函数y=f（x）有两个极值点x₁ ， x₂ ，且x₁＜x₂ ，求证： $0 < \frac{f (x_{2})}{x_{1}} < - \frac{1}{2} + l n 2$ ．

查看试题解析
22. 平面直角坐标系xOy中，曲线C：（x﹣1）²+y²=1．直线l经过点P（m，0），且倾斜角为 $\frac{π}{6}$ ．以O为极点，以x轴正半轴为极轴，建立坐标系．
（Ⅰ）写出曲线C的极坐标方程与直线l的参数方程；
（Ⅱ）若直线l与曲线C相交于A，B两点，且|PA|•|PB|=1，求实数m的值．

查看试题解析
23. 已知函数f（x）=|x+6|﹣|m﹣x|（m∈R）
（Ⅰ）当m=3时，求不等式f（x）≥5的解集；
（Ⅱ）若不等式f（x）≤7对任意实数x恒成立，求m的取值范围．

查看试题解析

分数（分数段）	频数（人数）	频率
[60，70）	9	x
[70，80）	y	0.38
[80，90）	16	0.32
[90，100）	z	s
合计	p	1