2017年辽宁省沈阳市高考数学三模试卷（理科）

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题：

1. 若集合A={x|x≥0}，且A∩B=B，则集合B可能是（）

A、{1，2} B、{x|x≤1} C、{﹣1，0，1} D、R

查看试题解析
2. 已知i是虚数单位，则满足z﹣i=|1+2i|的复数z在复平面上对应点所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知双曲线 $\frac{x^{2}}{9} - \frac{y^{2}}{4} = 1$ ，则其焦距为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{5}$ C、 $\sqrt{13}$ D、 $2 \sqrt{13}$

查看试题解析
4. 已知向量 $\vec{a}$ 与 $\vec{b}$ 不共线， $\vec{A B} = \vec{a} + m \vec{b}$ ， $\vec{A C} = n \vec{a} + \vec{b}$ （m，n∈R），则 $\vec{A B}$ 与 $\vec{A C}$ 共线的条件是（）

A、m+n=0 B、m﹣n=0 C、mn+1=0 D、mn﹣1=0

查看试题解析
5. 若 $s i n α + 3 s i n (\frac{π}{2} + α) = 0$ ，则cos2α的值为（）

A、 $- \frac{3}{5}$ B、 $\frac{3}{5}$ C、 $- \frac{4}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 按如图所示的程序框图，若输入a=81，则输出的i=（）

A、14 B、17 C、19 D、21

查看试题解析
7. 《九章算术》是我国古代内容极为丰富的数学名著，书中提到了一种名为“刍甍”的五面体（如图）：面ABCD为矩形，棱EF∥AB．若此几何体中，AB=4，EF=2，△ADE和△BCF都是边长为2的等边三角形，则此几何体的表面积为（）

A、 $8 \sqrt{3}$ B、 $8 + 8 \sqrt{3}$ C、 $6 \sqrt{2} + 2 \sqrt{3}$ D、 $8 + 6 \sqrt{2} + 2 \sqrt{3}$

查看试题解析
8. 在如图所示的矩形中随机投掷30000个点，则落在曲线C下方（曲线C为正态分布N（1，1）的正态曲线）的点的个数的估计值为（）
附：正态变量在区间（μ﹣σ，μ+σ），（μ﹣2σ，μ+2σ），（μ﹣3σ，μ+3σ）内取值的概率分别是0.683，0.954，0.997．

A、4985 B、8185 C、9970 D、24555

查看试题解析
9. 已知直线 $\sqrt{3} x - y - \sqrt{3} = 0$ 与抛物线y²=4x交于A，B两点（A在x轴上方），与x轴交于F点， $\vec{O F} = λ \vec{O A} + μ \vec{O B}$ ，则λ﹣μ=（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
10. 已知某三棱锥的三视图如图所示，图中的3个直角三角形的直角边长度已经标出，则在该三棱锥中，最短的棱和最长的棱所在直线的成角余弦值为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 数列{a_n}的前n项和为S_n ， a₁=1， $a_{n} + a_{n + 1} = 3 \times 2^{n - 1}$ ，则S₂₀₁₇=（）

A、2²⁰¹⁸﹣1 B、2²⁰¹⁸+1 C、2²⁰¹⁷﹣1 D、2²⁰¹⁷+1

查看试题解析
12. 已知函数f（x）=ln（1+x）﹣ln（1﹣x），给出以下四个命题：
①∀x∈（﹣1，1），有f（﹣x）=﹣f（x）；
②∀x₁ ， x₂∈（﹣1，1）且x₁≠x₂ ，有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > 0$ ；
③∀x₁ ， x₂∈（0，1），有 $f (\frac{x_{1} + x_{2}}{2}) \leq \frac{f (x_{1}) + f (x_{2})}{2}$ ；
④∀x∈（﹣1，1），|f（x）|≥2|x|．
其中所有真命题的序号是（）

A、①② B、③④ C、①②③ D、①②③④

查看试题解析

二、填空题：

13. 已知函数f（x）= ${\begin{matrix} l o g_{2} x ， x > 0 \\ {(\frac{1}{3})}^{x} ， x \leq 0 \end{matrix}$ ，则f[f（ $\frac{1}{4}$ ）]的值为．

查看试题解析
14. （1+2x）³（1﹣x）⁴展开式中x²的系数为．

查看试题解析
15. 某班共46人，从A，B，C，D，E五位候选人中选班长，全班每人只投一票，且每票只选一人．投票结束后（没人弃权）：若A得25票，B得票数占第二位，C、D得票同样多，得票最少的E只得4票，那么B得票的票数为．

查看试题解析
16. 已知点 $P (x ， y) 满足 {\begin{matrix} x + y \geq 4 \\ y \leq x + 2 \\ x \leq 3 \end{matrix}$ ，点A，B是圆x²+y²=2上的两个点，则∠APB的最大值为．

查看试题解析

三、解答题：

17. 已知函数 $f (x) = 2 s i n (2 x + φ) (| φ | < \frac{π}{2})$ 部分图象如图所示．
（Ⅰ）求φ值及图中x₀的值；
（Ⅱ）在△ABC中，A，B，C的对边分别为a，b，c，已知 $c = \sqrt{7}$ ，f（C）=﹣2，sinB=2sinA，求a的值．

查看试题解析
18. “共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图：
（Ⅰ）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；
（Ⅱ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；
A
B
合计
认可
不认可
合计
（Ⅲ）若从此样本中的A城市和B城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自B城市的概率是多少？
附：参考数据：
（参考公式： $Χ^{2} = \frac{n {(n_{11} n_{22} - n_{12} n_{21})}^{2}}{n_{1 +} n_{2 +} n_{+ 1} n_{+ 2}}$ ）

查看试题解析
19. 如图，在三棱柱ABC﹣A₁B₁C₁中，侧面AA₁B₁B⊥底面ABC，△ABC和△ABB₁都是边长为2的正三角形．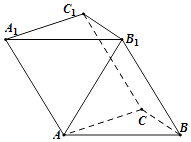
（Ⅰ）过B₁作出三棱柱的截面，使截面垂直于AB，并证明；
（Ⅱ）求AC₁与平面BCC₁B₁所成角的正弦值．

查看试题解析
20. 已知定直线l：y=x+3，定点A（2，1），以坐标轴为对称轴的椭圆C过点A且与l相切．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）椭圆的弦AP，AQ的中点分别为M，N，若MN平行于l，则OM，ON斜率之和是否为定值？若是定值，请求出该定值；若不是定值请说明理由．

查看试题解析
21. 已知f（x）=e^x与g（x）=ax+b的图象交于P（x₁ ， y₁），Q（x₂ ， y₂）两点．
（Ⅰ）求函数h（x）=f（x）﹣g（x）的最小值；
（Ⅱ）且PQ的中点为M（x₀ ， y₀），求证：f（x₀）＜a＜y₀ ．

查看试题解析
22. 已知曲线C的参数方程为 ${\begin{matrix} x = 2 c o s θ \\ y = \sqrt{3} s i n θ \end{matrix} (θ 为参数)$ ，在同一平面直角坐标系中，将曲线C上的点按坐标变换 ${\begin{matrix} x' = \frac{1}{2} x \\ y' = \frac{1}{\sqrt{3}} y \end{matrix}$ 得到曲线C'，以原点为极点，x轴的正半轴为极轴，建立极坐标系．
（Ⅰ）求曲线C'的极坐标方程；
（Ⅱ）若过点 $A (\frac{3}{2} ， π)$ （极坐标）且倾斜角为 $\frac{π}{6}$ 的直线l与曲线C'交于M，N两点，弦MN的中点为P，求 $\frac{| A P |}{| A M | \cdot | A N |}$ 的值．

查看试题解析
23. 已知正实数a，b，c，函数f（x）=|x+a|•|x+b|．
（Ⅰ）若a=1，b=3，解关于x的不等式f（x）+x+1＜0；
（Ⅱ）求证：f（1）f（c）≥16abc．

查看试题解析

	A	B	合计
认可
不认可
合计