2017年江西省鹰潭市高考数学二模试卷（理科

试卷更新日期：2017-07-30 类型：高考模拟

进入出卷网下载

一、选择题：

1. 设集合A={x| $\frac{2}{x - 1}$ ≥1}，B={y|y=log₂x，0＜x≤4}，则A∩B=（）

A、∅ B、（1，2] C、（﹣∞，1） D、[2，3]

查看试题解析
2. “Z= $\frac{1}{s i n θ + c o s θ \cdot i}$ ﹣ $\frac{1}{2}$ （其中i是虚数单位）是纯虚数．”是“θ= $\frac{π}{6}$ +2kπ”的（）条件．

A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要

查看试题解析
3. 等差数列{a_n}的前n项和是S_n ，且a₃=1，a₅=4，则S₁₃=（）

A、39 B、91 C、48 D、51

查看试题解析
4. 我们知道：“平面中到定点等于定长的点轨迹是圆”拓展至空间：“空间中到定点的距离等于定长的点的轨迹是球”，类似可得：已知A（﹣1，0，0），B（1，0，0），则点集{P（x，y，z）||PA|﹣|PB|=1}在空间中的轨迹描述正确的是（）

A、以A，B为焦点的双曲线绕轴旋转而成的旋转曲面 B、以A，B为焦点的椭球体 C、以A，B为焦点的双曲线单支绕轴旋转而成的旋转曲面 D、以上都不对

查看试题解析
5. 余江人热情好客，凡逢喜事，一定要摆上酒宴，请亲朋好友、同事高邻来助兴庆贺．欢度佳节，迎亲嫁女，乔迁新居，学业有成，仕途风顺，添丁加口，朋友相聚，都要以酒示意，借酒表达内心的欢喜．而凡有酒宴，一定要划拳，划拳是余江酒文化的特色．余江人划拳注重礼节，形式多样；讲究规矩，蕴含着浓厚的传统文化和淳朴的民俗特色．在礼节上，讲究“尊老尚贤敬远客”一般是东道主自己或委托桌上一位酒量好的划拳高手来“做关”，﹣﹣就是依次陪桌上会划拳的划一年数十二拳（也有半年数六拳）．十二拳之后晚辈还要敬长辈一杯酒．
再一次家族宴上，小明先陪他的叔叔猜拳12下，最后他还要敬他叔叔一杯，规则如下：前两拳只有小明猜赢叔叔，叔叔才会喝下这杯敬酒，且小明也要陪喝，如果第一拳小明没猜到，则小明喝下第一杯酒，继续猜第二拳，没猜到继续喝第二杯，但第三拳不管谁赢双方同饮自己杯中酒，假设小明每拳赢叔叔的概率为 $\frac{1}{3}$ ，问在敬酒这环节小明喝酒三杯的概率是多少（）
（猜拳只是一种娱乐，喝酒千万不要过量！）

A、 $\frac{4}{9}$ B、 $\frac{8}{27}$ C、 $\frac{2}{9}$ D、 $\frac{4}{27}$

查看试题解析
6. 函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，则下列有关f（x）性质的描述正确的是（）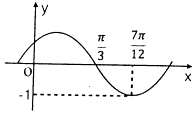

A、φ= $\frac{2 π}{3}$ B、x= $\frac{7 π}{12}$ +kπ，k∈Z为其所有对称轴 C、[ $\frac{π}{12}$ + $\frac{k π}{2}$ ， $\frac{7 π}{12}$ + $\frac{k π}{2}$ ]，k∈Z为其减区间 D、f（x）向左移 $\frac{π}{12}$ 可变为偶函数

查看试题解析
7. 若 $\frac{1}{a}$ ＜ $\frac{1}{b}$ ＜0，则下列结论正确的是（）

A、a²＞b² B、1＞（ $\frac{1}{2}$ ）^b＞（ $\frac{1}{2}$ ）^a C、 $\frac{b}{a}$ + $\frac{a}{b}$ ＜2 D、ae^b＞be^a

查看试题解析
8. 已知有下面程序，若程序执行后输出的结果是11880，则在程序后面的“横线”处应填（）

A、i≥9 B、i=8 C、i≥10 D、i≥8

查看试题解析
9. 已知x，y满足 ${\begin{matrix} x + y \geq 4 \\ x^{2} + y^{2} \leq 16 \end{matrix}$ ，则z=x²+6x+y²+8y+25的取值范围是（）

A、[ $\frac{121}{2}$ ，81] B、[ $\frac{121}{2}$ ，73] C、[65，73] D、[65，81]

查看试题解析
10. 如图是某几何体挖去一部分后得到的三视图，其中主视图和左视图相同都是一个等腰梯形及它的内切圆，俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心．问该几何体的体积是（）

A、 $\frac{420 - 32 π}{3}$ B、 $\frac{336 - 32 π}{3}$ C、 $\frac{168 - 4 π}{3}$ D、 $\frac{168 \sqrt{2} - 64 \sqrt{2} π}{3}$

查看试题解析
11. 已知抛物线x²=2py和 $\frac{x^{2}}{2}$ ﹣y²=1的公切线PQ（P是PQ与抛物线的切点，未必是PQ与双曲线的切点）与抛物线的准线交于Q，F（0， $\frac{P}{2}$ ），若 $\sqrt{2}$ |PQ|= $\sqrt{3}$ |PF|，则抛物线的方程是（）

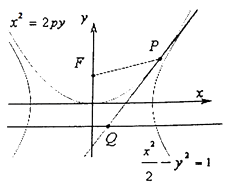A、x²=4y B、x²=2 $\sqrt{3}$ y C、x²=6y D、x²=2 $\sqrt{2}$ y

查看试题解析
12. f（x）=|x﹣2017|+|x﹣2016|+…+|x﹣1|+|x+1|+…+|x+2016|+|x+2017|，在不等式e^2017x≥ax+1（x∈R）恒成立的条件下等式f（2018﹣a）=f（2017﹣b）恒成立，求b的取值集合（）

A、{b|2016≤b≤2018} B、{2016，2018} C、{2018} D、{2017}

查看试题解析

二、填空题

13. 已知向量| $\vec{a}$ |=1， $\vec{a} \cdot \vec{b}$ =1，则| $\vec{b}$ |_min= ．

查看试题解析
14. 数列{a_n}的前n项和是S_n ， a₁=1，2S_n=a_n+1（n∈N₊），则a_n= ．

查看试题解析
15. $\int_{0}^{x}$ （a₀+a₁x+a₂x²+…+a_nxⁿ）dx=x（x+1）ⁿ ，则a₁+a₂+…+a_n= ．

查看试题解析
16. 直线l与函数y=cosx（x∈[﹣ $\frac{π}{2}$ ， $\frac{π}{2}$ ]）图象相切于点A，且l∥CP，C（﹣ $\frac{π}{2}$ ，0），P为图象的极值点，l与x轴交点为B，过切点A作AD⊥x轴，垂足为D，则 $\vec{B A} \cdot \vec{B D}$ = ．

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C的对边分别为a，b，c，并且b=2

(1)、若角A，B，C成等差数列，求△ABC外接圆的半径；

(2)、若三边a，b，c成等差数列，求△ABC内切圆半径的最大值．

查看试题解析
18. 如图半圆柱OO₁的底面半径和高都是1，面ABB₁A₁是它的轴截面（过上下底面圆心连线OO₁的平面），Q，P分别是上下底面半圆周上一点．

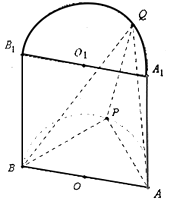(1)、证明：三棱锥Q﹣ABP体积V_Q_﹣ABP≤ $\frac{1}{3}$ ，并指出P和Q满足什么条件时有AP⊥BQ

(2)、求二面角P﹣AB﹣Q平面角的取值范围，并说明理由．

查看试题解析

19. 鹰潭市龙虎山花语世界位于中国第八处世界自然遗产，世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区﹣﹣龙虎山主景区排衙峰下，是一座独具现代园艺风格的花卉公园，园内汇集了3000余种花卉苗木，一年四季姹紫嫣红花香四溢．花园景观融合法、英、意、美、日、中六大经典园林风格，景观设计唯美新颖．玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致，交相呼应又自成一体，是世界园艺景观的大展示．该景区自2015年春建成试运行以来，每天游人如织，郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人．

某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议，特别在2017年4月1日赏花旺季对进园游客进行取样调查，从当日12000名游客中抽取100人进行统计分析，结果如下：（表一）

年龄	频数	频率	男	女
[0，10）	10	0.1	5	5
[10，20）	①	②	③	④
[20，30）	25	0.25	12	13
[30，40）	20	0.2	10	10
[40，50）	10	0.1	6	4
[50，60）	10	0.1	3	7
[60，70）	5	0.05	1	4
[70，80）	3	0.03	1	2
[80，90）	2	0.02	0	2
合计	100	1.00	45	55

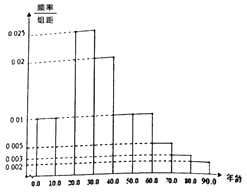(1)、完成表格一中的空位①﹣④，并在答题卡中补全频率分布直方图，并估计2017年4月1日当日接待游客中30岁以下人数．

(2)、完成表格二，并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关？

(3)、按分层抽样（分50岁以上与50以下两层）抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票，再从这10人中选取2人接受电视台采访，设这2人中年龄在50岁以上（含）的人数为ξ，求ξ的分布列

（表二）

	50岁以上	50岁以下	合计
男生	5	40	45
女生	15	40	55
合计	20	80	100

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：k²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析

20. 已知A（﹣1，0），B（1，0）， $\vec{A P}$ = $\vec{A B}$ + $\vec{A C}$ ，| $\vec{A P}$ |+| $\vec{A C}$ |=4

(1)、求P的轨迹E

(2)、过轨迹E上任意一点P作圆O：x²+y²=3的切线l₁ ， l₂ ，设直线OP，l₁ ， l₂的斜率分别是k₀ ， k₁ ， k₂ ，试问在三个斜率都存在且不为0的条件下， $\frac{1}{k_{0}}$ （ $\frac{1}{k_{1}}$ + $\frac{1}{k_{2}}$ ）是否是定值，请说明理由，并加以证明．

查看试题解析
21. 已知函数f（x）=2lnx+ $\frac{a}{x}$ ﹣2lna﹣k $\frac{x}{a}$

(1)、若k=0，证明f（x）＞0

(2)、若f（x）≥0，求k的取值范围；并证明此时f（x）的极值存在且与a无关．

查看试题解析

四、解答题

22. 曲线C：ρ²﹣2ρcosθ﹣8=0 曲线E： ${\begin{matrix} x = t + 2 \\ y = k t + 1 \end{matrix}$ （t是参数）

(1)、求曲线C的普通方程，并指出它是什么曲线．

(2)、当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值．

查看试题解析

五、解答题

23. f（x）=|x+a|+|x﹣a²|，a∈（﹣1，3）

(1)、若a=1，解不等式f（x）≥4

(2)、若对∀x∈R，∃a∈（﹣1，3），使得不等式m＜f（x）成立，求m的取值范围．

查看试题解析