人教版初中数学2019-2020学年九年级上学期期末专题复习专题7：点、直线与圆的位置关系

试卷更新日期：2019-12-24 类型：复习试卷

进入出卷网下载

一、单选题

1. 半径为5的 $⊙ O$ ，圆心在直角坐标系的原点 $O$ ，则点 $P (3 ， 4)$ 与 $⊙ O$ 的位置关系是 $($ $)$

A、在 $⊙ O$ 上 B、在 $⊙ O$ 内 C、在 $⊙ O$ 外 D、不能确定

查看试题解析
2. 已知⊙O的半径为4cm，点P在⊙O上，则OP的长为（）

A、1cm B、2cm C、4cm D、8cm

查看试题解析
3. 如图，PA是⊙O的切线，A为切点，PO的延长线交⊙O于点B ，若∠B＝32°，则∠P的度数为（）

A、24º B、26º C、28º D、32º

查看试题解析
4. 如图，直线AB是⊙O的切线，点C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，则∠CED的度数为（）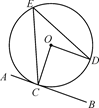

A、30° B、35° C、40° D、45°

查看试题解析

二、填空题

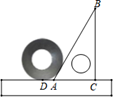
5. $Δ A B C$ 的两直角边长分别为6和8，则该 $Δ A B C$ 的外接圆的半径为．

查看试题解析
6. 在平面直角坐标系中有 $A$ ， $B$ ， $C$ 三点， $A (1, 3)$ ， $B (3, 3)$ ， $C (5, 1)$ ．现在要画一个圆同时经过这三点，则圆心坐标为．

查看试题解析
7. 把直尺、三角尺和圆形螺母按如图所示放置于桌面上，∠CAB=60°，若量出AD=6cm，则圆形螺母的外直径是.

查看试题解析

三、解答题

8. 如图，AB是圆O的直径，AC切圆O于点A，BC交圆O于点D，已知圆O的半径为6， $∠ C$ =40°，求弧AD的长.（结果保留 $π$ ）

查看试题解析
9. 如图，△ABC为等腰三角形，AB=AC，O是底边BC的中点，⊙O与腰AB相切于点D，求证：AC与⊙O相切．

查看试题解析

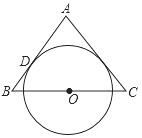
四、综合题

10. 如图，⊙O是△ABC的外接圆，AB经过点O，CD是弦，且CD⊥AB于点F，连接AD，过点B的直线与线段AD的延长线交于点E，且∠E=∠ACF．

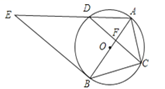(1)、若CD=2 $\sqrt{15}$ ， AF=3，求⊙O的周长；

(2)、求证：直线BE是⊙O的切线．

查看试题解析
11. 如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E.

(1)、求证：CE为⊙O的切线；

(2)、判断四边形AOCD的形状，并说明理由.

查看试题解析
12. 如图，在平面直角坐标系中，点A、C的坐标分别为（0，8）、（6，0），以AC为直径作⊙O，交坐标轴于点B，点D是⊙O 上一点，且 $\overset{⌢}{B D} = \overset{⌢}{A D}$ ，过点D作DE⊥BC，垂足为E.

(1)、求证：CD平分∠ACE；

(2)、判断直线ED与⊙O的位置关系，并说明理由；

(3)、求线段CE的长.

查看试题解析