人教版初中数学2019-2020学年九年级上学期期末专题复习 专题6：圆的有关性质

试卷更新日期：2019-12-24 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 下列命题中，是真命题的是 (    )
    A、三点确定一个圆   B、相等的圆周角所对的弧相等   C、平分弦的直径垂直于弦   D、90° 的圆周角所对的弦是直径

    查看试题解析

  • 2. 如图等腰三角形的顶角 ∠A =45°，以AB为直径的半圆O与BC，AC相较于点D，E两点，则弧AE所对的圆心角的度数为（      ）

    A、40° B、50° C、90° D、100°

    查看试题解析

  • 3. 下列四个命题中，①圆的对称轴是直径；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．正确的有（   ）
    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 4. 如图，AB为⊙O的弦，过点O作AB的垂线，交AB于点C，交⊙O于点D，已知⊙O的直径为10，CD=2，则AB的长为（ ）

    A、4 B、6 C、8 D、10

    查看试题解析

  • 5. 如图，已知∠AOB是⊙O的圆心角，∠AOB=60°，则圆周角∠ACB的度数是（ ）

    A、50° B、25° C、100° D、30°

    查看试题解析

二、填空题

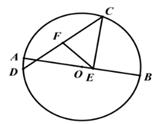
  • 6. 在半径为5的⊙O中，弦AB的长为5，则∠AOB＝.

    查看试题解析

  • 7. 如图，AB是⊙O的直径，C、D是⊙O上的两个动点(点C、D不与A、B重合)，在运动过程中弦CD始终保持不变，F是弦CD的中点，过点C作CE⊥AB于点E．若CD=5，AB=6，当EF取得最大值时，CE的长度为 。

    查看试题解析

  • 8. 如图，在⊙O中，CD⊥AB于E，若∠BAD=30°，且BE=1，则CD=.

    查看试题解析

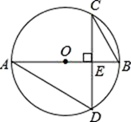  • 9. 已知 ⊙O 的半径为2， ⊙O 中有两条平行的弦 AB 和 CD ， AB=2 ， CD=23 ，则两条弦之间的距离为 ．

    查看试题解析

三、解答题

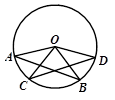
  • 10. 已知：如图，在⊙O中，弦AB=CD．求证：∠AOC =∠BOD．

    查看试题解析

  • 11. 如图，请用尺规作图的方法做出以MN为直径的圆A（保留作图痕迹，不写做法）

    查看试题解析

四、综合题

  • 12. 如图，AE是⊙O的直径，半径OC⊥弦AB，点D为垂足，连BE、EC。

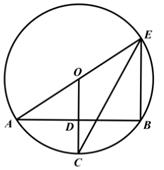    (1)、若∠BEC=26°，求∠AOC的度数；
    (2)、若∠CEA=∠A，EC=6，求⊙O的半径。

    查看试题解析

  • 13. 如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，连接AC、FC.

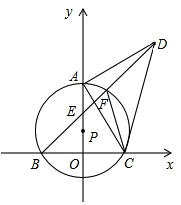    (1)、求证：∠ACF=∠ADB；
    (2)、若点A到BD的距离为m，BF+CF=n，求线段CD的长；
    (3)、当⊙P的大小发生变化而其他条件不变时， DEAO 的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由.

    查看试题解析

  • 14. 如图，△ABC内接于⊙O，AB=AC，∠BAC=36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F.

    (1)、求∠DAF的度数；
    (2)、求证：AE2=EF•ED；

    查看试题解析