浙江省宁波七中教育集团2020届九年级上学期数学第二次月考试卷
试卷更新日期：2019-12-24 类型：月考试卷
一、选择题(本大题共有12小题，每题4分，共48分)
-
1. “明年的12月4日是晴天”这个事件是（ ）A、确定事件 B、不可能事件 C、必然事件 D、不确定事件2. 如图，DE∥BC，AD：DB=2：1，那么△ADE与△ABC的相似比为（ ）
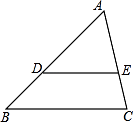A、 B、 C、 D、23. 如图，已知A，B，C在⊙O上， 的度数为300°，∠C的度数是（ ）
A、30° B、40° C、50° D、60°4. 黑色不透明口袋里装有红色、白色球共10个，它们除颜色外都相同.从口袋中随机摸出一个球，记下颜色后放回，并摇匀，不断重复上述实验1000次，其中200次摸到红球，则可估计口袋中红色球的个数是（ ）A、2 B、4 C、6 D、85. 抛物线y=x2-2x-m2(m是常数）的顶点在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图，路灯距地面8米，身高1.6米的小明从距离路灯的底部(点O)20米的点A处沿OA所在的直线行走14米到点B时，人影长度（ ）A、变长3.5米 B、变长2.5米 C、变短3.5米 D、变短2.5米7. 在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点)，如果以A为圆心，r为半径画圆；选取的格点中除点A外恰好有4个点在圆内，则r的取值范围为（ ）
A、 <r< B、 <r≤ C、 <r≤5 D、5<r<8. 已知抛物线y= x2+1其有如下性质：抛物线上任意一点到定点F(0，2)的距离与到x轴的距离相等，点M的坐标为(3，6)，P是抛物线y= x2+1上一动点，则△PMF周长的最小值是（ ）
A、5 B、9 C、11 D、139. 一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了1.4m，则此时排水管水面宽为（ ）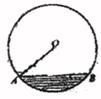
A、1.2m B、1.4m C、1.6m D、1.8m10. 如图，AD∥BC，∠D=90°，AD=2，BC=5，DC=11，若在边DC上有点P，使△PAD与△PBC相似，则这样的点P有（ ）
A、1个 B、2个 C、3个 D、4个11. 函数y=x2+bx+c与y=x的图象如图所示，有以下结论：①b2-4c>0：②b+c+1=0；③3b+c+6=0：④当1<x<3时，x2+(b-1)x+c<0．其中正确的个数为（ ）
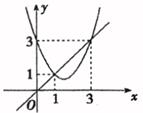A、1 B、2 C、3 D、412. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x，y)的对应值如下表所示：x
…
0
4
…
y
…
0.37
-1
0.37
…
则方程ax2+bx+1.37=0的根是（ ）
A、0或4 B、 或4- C、1或5 D、无实根二、填空题(每空4分，共24分)
-
13. 若a：b=3：2，且3a-2b=4，则a+b=。14. 已知⊙O的半径为1，则其内接正六边形的边长为.15. 合作小组的4位同学坐在课桌旁讨论问题，学生A的座位如图所示，学生B，C，D随机坐到其他三个座位上，求学生B坐在2号座位且C坐3号座位的概率是.
16. 在Rt△ABC纸片上剪出9个如图所示的正方形，点E，F落在AB边上，每个正方形的边长为1，则Rt△ABC的面积为。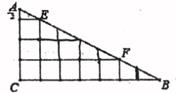
17. 如图，△ABC∽△ADE，∠BAC=∠DAE=90°，AB=16，AC=12，F是DE的中点，若点E是直线BE上的动点，连接BF，则BF的最小值是。
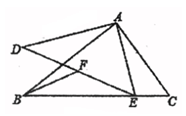18. 如图2×2网格(每个小正方形的边长为l)中有A，B，C，D，E，F，G，H，O九个格点．抛物线l的解析式为y=(-1)nx2+bx+c(n为整数)．若l经过这九个格点中的三个，则满足这样条件的抛物线条数为 条。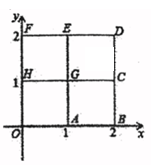
三、解答题(第19题7分，第20题9分，第21-23题8分，第24-25题12分，第26题14分，共78分)
-
19. 如图，在菱形ABCD中，点E在边CD上，连结AE并延长与BC的延长线交于点F。
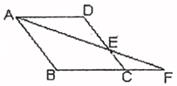(1)、写出图中所有的相似三角形(不需证明)；(2)、若菱形ABCD的边长为6，DE：AB=3：5，试求CF的长。20. 已知抛物线y=x2+(n-3)x+n+1经过坐标原点O，与x轴交于另一点A，顶点为B．求：(1)、抛物线的解析式；(2)、△AOB的面积；(3)、要使二次函数的图象过点(10，0)，应把图象沿x轴向右平移个单位。21. 在-2，-1，0，1，2这五个数中任意取两个数m，n，已知有二次函数y=(x-m)2+n。(1)、先取了m=1，则从余下的数中任意取n，求二次函数图象与y轴交于负半轴的概率；(2)、任意取两个数m，n，求二次函数y=(x-m)2+n的顶点在坐标轴上的概率。22. 如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成矩形零件 PQMN，使矩形PQMN的边QM在BC上，其余两个顶点P，N分别在AB，AC上。
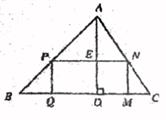(1)、当矩形的边PN=PQ时，求此时矩形零件PQMN的面积；(2)、求这个矩形零件PQMN面积S的最大值。23. 在△ABC中，AB=AC，点A在以BC为直径的半圆内，请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹)
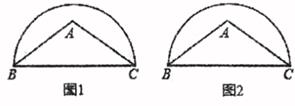(1)、在图1中作弦EF，使EF∥BC；(2)、在图2中作出圆心O．24. 某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售，已知加工过程中质量损耗了40%，该商户对该茶叶试销期间，销售单价不低于成本单价，且每千克获利不得高于成本单价的60%，经试销发现，每天的销售量y(千克)与销售单价x(元/千克)符合一次函数y=kx+b，且x=35时，y=45；x=42时，y=38。(1)、求一次函数y=kx+b的表达式；(2)、若该商户每天获得利润不计加工费用)为W元，试写出利润W与销售单价x之间的关系式；销售单价每千克为多少元时，商户每天可获得最大利润，最大利润是多少元?(3)、若该商户每天获得利润不低于225元，试确定销售单价x的范围。25. 如图，AB是半圆O的直径，半径OC⊥AB，OB=2，D是OB的中点，点E是弧BC上的动点，连接AE，DE。
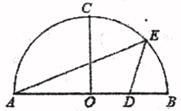(1)、当点E是弧BC的中点时，求△ADE的面积；(2)、若tan∠AED= ，求AE的长；(3)、点F是半径OC上一动点，设点E到直线OC的距离为m，当△DEF是等腰直角三角形时，求m的值；26. 已知如图，二次函数y=ax2+bx+2的图象经过A(3，3)，与x轴正半轴交于B点，与y轴交于C点，△ABC的外接圆恰好经过原点O。
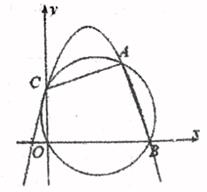(1)、求B点的坐标及二次函数的解析式；(2)、抛物线上一点Q(m，m+3)，(m为整数)，点M为△ABC的外接圆上一动点，求线段QM长度的范围；(3)、将△AOC绕平面内一点P旋转180°至△AOC(点O‘与O为对应点)，使得该三角形的对应点中的两个点落在y=ax2+bx+2的图象上，求出旋转中心P的坐标。