浙江省湖州市长兴县2020届九年级上学期数学第三次月考试卷

试卷更新日期：2019-12-24 类型：月考试卷

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. 如图，将图形用放大镜放大，所用的图形改变是（）

A、平移 B、轴对称 C、旋转 D、相似

查看试题解析
2. 已知⊙O的半径为5，若PO=4，则点P与⊙O的位置关系是（）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法判断

查看试题解析
3. 某校食堂每天中午为学生提供A，B，C三种套餐，小张从中随机选一种，恰好选中A套餐的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、 $\frac{2}{3}$

查看试题解析
4. 把抛物线y=x²向上平移3个单位，平移后抛物线的表达式是（）

A、y=x²-3 B、y=x²+3 C、y=(x+3)² D、y=(x-3)²

查看试题解析
5. 如果两个相似正五边形的面积比为1：100。则它们的边长比为（）

A、1：10000 B、1：50 C、1：10 D、1：100

查看试题解析
6. 如图，A，D是⊙O上的两点，BC是直径，若∠D=20°，则∠OAB的度数是（）

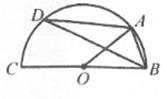A、40° B、50° C、70° D、80°

查看试题解析
7. 抛物线y=-x²+2x-c过A(-1，y₁)，B(2，y₂)，C(5，y₃)三点。则将y₁ ， y₂ ， y₃ ，从小到大顺序排列是（）

A、y₁<y₂<y₃ B、y₂<y₁<y₃ C、y₃<y₁<y₂ D、y₂<y₃<y₁

查看试题解析
8. 如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）

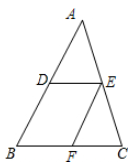A、 $\frac{A D}{A B} = \frac{A E}{A C}$ B、 $\frac{C E}{C F} = \frac{E A}{F B}$ C、 $\frac{D E}{B C} = \frac{A D}{B D}$ D、 $\frac{E F}{A B} = \frac{C F}{C B}$

查看试题解析
9. 如图，在正方形ABCD中，以A为圆心，AB为半径作 $\overset{⌢}{B D}$ ，交对角线AC于点E，连结BE并延长交CD于点F，记图中分割部分的面积为S₁ ， S₂ ．则下列对S₁与S₂的大小关系判断正确的是（）

A、S₁>S₂ B、S₁<S₂ C、S₁=S₂ D、与正方形ABCD的边长有关

查看试题解析
10. 如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+c(a>0)与x轴的正半轴交于A，C两点(点A在点C右侧)，与y轴正半轴交于点B，连结BC，将△BOC沿直线BC翻折，若点O恰好落在线段AB上，则称该抛物线为”折点抛物线”，下列抛物线是“折点抛物线”的是（）

A、 $y = \frac{3}{4} x^{2} - \frac{11}{4} x + \frac{8}{3}$ B、 $y = \frac{4}{3} x^{2} - \frac{13}{3} x + 3$ C、 $y = \frac{3}{4} x^{2} - \frac{15}{4} x + 3$ D、 $y = \frac{4}{3} x^{2} - \frac{11}{3} x + \frac{9}{4}$

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

11. 已知二次函数y=ax²+1(a≠0)有最大值1，则a=。(写一个适当的值即可)

查看试题解析
12. 正十二边形的一个内角度数是°。

查看试题解析
13. 在比例尺为1：30000的城市交通地图上。一条道路的长为5cm，则它的实际长度为。

查看试题解析
14. 在澡堂上，老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀，让全班同学依次进行摸球试验，每次随机摸出一个球，记下颜色再放回搅匀，下表是试验得到的一组数据。
摸球的次数n
100
150
200
500
800
摸到黑球的次数m
26
37
49
124
200
摸到黑球的频率m/n
0.26
0.247
0.245
0.248
0.25
根据实验数据，可估计口袋中白球的个数是。

查看试题解析
15. 如图，在Rt△ABC中，∠BAC=90°，点D为BC中点，将△ABD绕点A按逆时针方向旋转50°，记点D在旋转过程中所经过的路径长为m，将△ABD绕点C按顺时针方向旋转100°，则点D在旋转过程中所经过的路径长为。(用含m的代数式表示)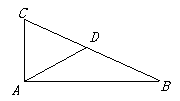

查看试题解析
16. 如图，在Rt△ABC中，已知AC=3，BC=4，点M是AB边上的一个动点，∠DME的两边与折线A—C—B分别交于点D和点E(点E在点D的右边)，且∠DME=∠A，若能使以点D，E，M为顶点的三角形与△ABC相似的点D有三个，则AM的长度x的取值范围是。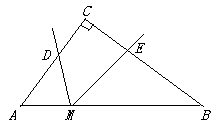

查看试题解析

三、解答题(本题有8小题，共66分)

17. 已知 $\frac{a}{b} = \frac{2}{3}$

(1)、求： $\frac{a}{a + 2 b}$

(2)、求证： $\frac{a}{a + 2 b} = \frac{b}{3 a + 2 b}$

查看试题解析
18. 抛物线y=x²-(m+1)x+m与y轴交于(0，-3)点。

(1)、求出m的值和抛物线与x轴的交点；

(2)、x取什么值时，y>0?

查看试题解析
19. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于A，B，C，直线DF分别交l₁ ， l₂ ， l₃于D，E，F，若 $\frac{A B}{A C} = \frac{1}{3}$ ，EF=6，求DE的长。

查看试题解析
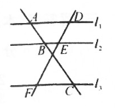20. 一个不透明的布袋中有分别标有汉字“我””的”“祖”国”的四个小球，除汉字外没有任何区别，每次摸球前先摇匀再摸球。

(1)、若从中任意摸一个球，求摸出球上的汉字刚好是”国”字的概率；

(2)、小林从中任取一个球，记下汉字后放回，摇匀后再从中任取一个。请用树状图或列表法，求小林取出的两个球上的汉字恰好能组成“祖国”的概率。

查看试题解析
21. 如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=62°， ∠APD=86°。

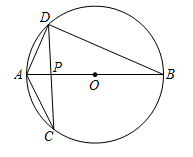(1)、求∠B的大小；

(2)、已知AD=6，求圆心O到BD的距离。

查看试题解析
22. 金秋时节，硕果飘香，某精准扶贫项目果园上市一种有机生态水果，为帮助果园拓宽销路。欣欣超市对这种水果进行代销，进价为5元／千克，售价为6元／千克时，当天的销售量为60千克；在销售过程中发现：销售单价每上涨0.5元，当天的销售量就减少5千克．设当天销售单价统一为x元／千克(x≥6，且x按0.5元的倍数上涨)，当天销售利润为y元。

(1)、求y与x的函数关系式；

(2)、若该种水果每千克的利润不超过80％，求当天获得利润的范围。

查看试题解析
23. 如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G。点E，F分别是CD与DG上的点，连结EF。

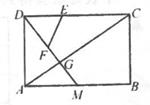(1)、求证：CG=2AG；

(2)、若DE=6，当以E，F，D为顶点的三角形与△CDG相似时，求EF的长；

(3)、若点E从点D出发，以每秒2个单位的速度向点C运动，点F从点G出发，以每秒1个单位的速度向点D运动。当一个点到达，另一个随即停止运动。在整个运动过程中，求四边形CEFG的面积的最小值。

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线y=ax²+8ax(a>0)与x轴交于O，A两点，顶点为M，对称轴与x轴交于H，与过O，A，M三点的⊙Q交于点B，⊙Q的半径为5，点C从点B出发，沿着圆周顺时针向点M运动，射线MC与x轴交于D，与抛物线交于E，过点E作ME的垂线交抛物线的对称轴于点F。

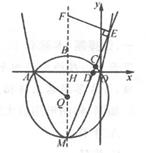(1)、求抛物线的解析式；

(2)、当点C的运动路径长为 $\frac{10 π}{3}$ 时，求证：HD=2 $\sqrt{3}$ HA。

(3)、在点C运动过程中．是否存在这样的位置，使得以点M，E，F为顶点的三角形与△AHQ相似?若存在，求出此位置时点E的坐标；若不存在，请说明理由。

查看试题解析

摸球的次数n	100	150	200	500	800
摸到黑球的次数m	26	37	49	124	200
摸到黑球的频率m/n	0.26	0.247	0.245	0.248	0.25